Have you ever heard of the word "six degrees of separation"? It is said that two individuals are connected by at most five others. Lee is wondering about this and he wants to check it via the world's biggest friendship web called Koobecaf.
On Koobecaf, if A and B are friends, so are B and C, but either A or C knows the others, we say A and C are connected by one others, that's, B. The following pictures shows this case.

And the following one shows that 1 can reach 8 via five others. (Hmm... It is the first case of the sample input below.)
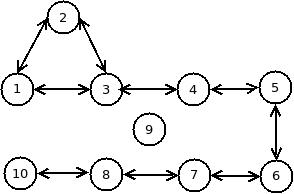
Now Lee will randomly pick two individuals and please help him check if the two are connected by less than six others.
输入
Input will consist of multiple test cases. Then for each test case:
- One line with two integers n and m, where n is the number of users on the Koobecaf (2 ≤ n ≤ 1000) and m is the number of pairs of friends (0 ≤ m ≤ 106).
- m lines following. Each line contains two integers A and B, denoted that A and B are friends (1 ≤ A, B ≤ n, A != B). It is guarantee that each pair is unique. And of course, "A B" is the same as "B A", thus they won't exist at the same time.
- The last line contains two integers X and Y, the two individuals to check (1 ≤ X, Y ≤ n, X != Y).
输出
For each case, output "YES" (without quotation marks) if X and Y are connected by at most five others, or "NO" otherwise.
样例输入
10 9
1 2
2 3
3 1
3 4
4 5
5 6
6 7
7 8
8 10
1 8
10 9
1 2
2 3
3 1
3 4
4 5
5 6
6 7
7 8
8 10
1 10
样例输出
YES
NO
大致题意:给定n个人和m对关系 最后给定2个人 问是否两人之间相隔不超过6人。
#include<bits/stdc++.h> #define inf 1<<29 #define CL(a,b) memset(a,b,sizeof(a)) using namespace std; const int N=1010; int n,m,a,b; int Map[N][N]; bool vis[N]; int dist[N]; int dijkstra(int x,int y) { CL(vis,false); for(int i=1;i<=n;i++) dist[i]=inf; dist[x]=0; while(1){ int v=-1; for(int u=1;u<=n;u++) if(!vis[u]&&(v==-1||dist[u]<dist[v])) v=u; if(v==-1) break; vis[v]=true; for(int u=1;u<=n;u++) dist[u]=min(dist[u],dist[v]+Map[v][u]); } return dist[y]; } int main() { while(~scanf("%d%d",&n,&m)){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++) Map[i][j]=Map[j][i]=inf; Map[i][i]=0; } for(int i=0;i<m;i++){ scanf("%d%d",&a,&b); Map[a][b]=Map[b][a]=1; } scanf("%d%d",&a,&b); if(dijkstra(a,b)>=7) printf("NO "); else printf("YES "); } return 0; }