


我们用dp[i][0/1][0/1]表示还剩最后i道题没切,目前主动权在小Z/小G手上,小Z/小G获得的最大收益
但好像不用记第3维,拿前缀和一减就算出来了(反正我打题的时候记了第3维)
怎么dp呢?
我们发现,当前小Z/小G有两种选择,
1自己切这道题,把主动权给对方(假设此时主动权在小Z手上,即dp[i][0][0]=dp[i+1][1][0]+d[i])
2让对方切这道题,主动权还在自己手上(假设此时主动权在小Z手上,即dp[i][0][0]=dp[i+1][0][0])
显然,拥有主动权的人肯定会选这两种方案的最大值(假设此时主动权在小Z手上,即dp[i][0][0]=max(dp[i+1][1][0]+d[i],dp[i+1][0][0]),即另一个人(小G)为dp[i][0][1]=dp[i+1][1][1]或dp[i+1][0][1]+d[i](看掌握主动权的那个人选哪种)
然后记搜一下就完了

#include<iostream> #include<cstdio> #include<cstring> using namespace std; struct xxx{int a[2];}dp[50100][2]; int b[50100],n; xxx DP(int T,int i) { if(T==n+1) { xxx xx;xx.a[0]=0;xx.a[1]=0;return xx; } if(dp[T][i].a[0]!=-1)return dp[T][i]; xxx c=DP(T+1,i);xxx d=DP(T+1,i^1); if(c.a[i]>d.a[i]+b[T]) dp[T][i].a[i]=c.a[i],dp[T][i].a[i^1]=c.a[i^1]+b[T]; else dp[T][i].a[i]=d.a[i]+b[T],dp[T][i].a[i^1]=d.a[i^1]; // cout<<T<<" "<<i<<" "<<dp[T][i].a[0]<<" "<<dp[T][i].a[1]<<endl; return dp[T][i]; } int main() { freopen("problem.in","r",stdin);freopen("problem.out","w",stdout); memset(dp,-1,sizeof(dp)); scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&b[i]); xxx aa=DP(1,0); cout<<aa.a[0]<<" "<<aa.a[1]; return 0; }



一开始把题目看成长方形的了,想了老半天。。。
先说一下题意,这道题题意有点难懂
有一个正方形网格,2~n-1行的第1列和第n列,和2~n-1列的第1行和第n行可以发车,每辆车速度相等且只能一直横着走或一直竖着走,不能拐弯,且你发的车不能相撞(即不同的车不能在同一时刻到达同一格),有一些格子有障碍,且车也不能撞障碍,求最多能发几辆车
 样例
样例
我们发现,由于正方形是对称的,所以影响关系其实会形成一个环,即下图中绿色地点发车的车不会撞到不在绿色位置发车的车,但它们可能会互相撞到。
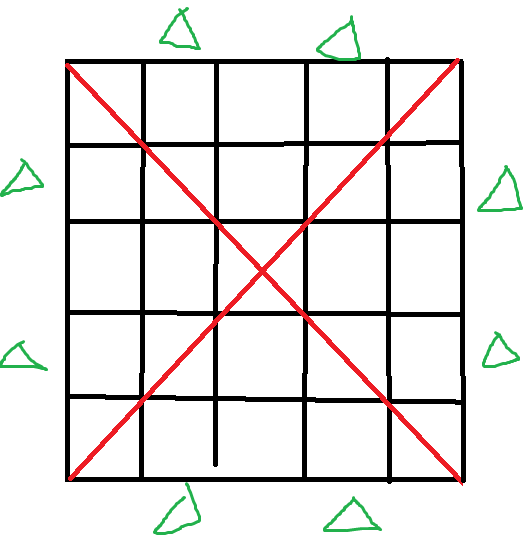
即每个行i只会与行n-i+1,列i,列n-i+1有关
显然,对于这8个发车地点,我们最多能选4个使得它们不相撞,即选蓝色的4个或绿色的4个都可以
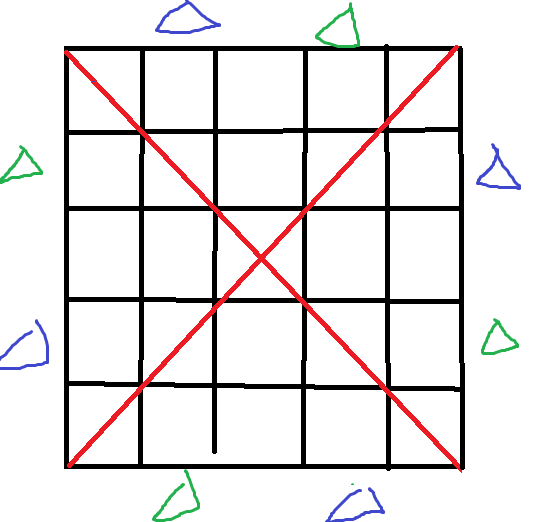
但是,如果有障碍在这两行两列上的话,则该行/列不能发车
然后我们从2~n/2,看看最多能发几辆车,计算答案即可。
若n是奇数,则第n/2+1行或n/2+1列上没有障碍,那么它对答案的贡献就是1,否则就是0

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int a[200100],b[200100]; int main() { freopen("car.in","r",stdin);freopen("car.out","w",stdout); int n,m,ans=0;scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);a[x]=1;b[y]=1;} for(int i=2;i+i<=n;i++) { int j=n-i+1; ans+=4-a[i]-a[j]-b[i]-b[j]; } if(n&1)ans+=1-(a[n/2+1]&b[n/2+1]); printf("%d",ans); return 0; }



首先,我们要认识gcd的几个性质:
1、gcd没有逆运算(和max一样),即你不可能用gcd的结果来求出原数,这就导致了无法前缀和
2、gcd(a,b)==gcd(c,b)(a==c),但是当a!=c时,gcd(a,b)也有可能等于gcd(c,b)。
对于每个右端点,任取左端点,其对应的区间的gcd只有log种,从左向右推的同时维护每种gcd的左端点即可。
如何维护左端点?
我们用Gcd[i][0]表示第i种不同的gcd值,Gcd[i][1]表示该种值的最远的左端点(此时正在枚举右端点)
由于我们新来了一个元素,所以我们把Gcd数组的每个元素与a[i]取个gcd,然后再把Gcd数组新加入一个元素:a[i]。(表示a[i]也是一种不同的gcd值)但是有可能a[i]会与前面重复呢?没关系,我们待会还要去重。
那么这些Gcd有可能会相等,但是这里一定包含了以i为右端点,任取左端点的区间的所有不同种类的Gcd值(根据性质2)
然后去重,每种相同元素保留最远的左端点,统计答案。
时间复杂度O(n(logai)^2),由于这是最坏复杂度,实际上时间复杂度远远小于这个上界,所以能过。
ans记得要看long long

#include<iostream> #include<cstdio> using namespace std; int a[500100],Gcd[100][2],tot=0,ggcd[100][2]; int gcd(int a,int b) { if(b==0)return a; return gcd(b,a%b); } int main() { freopen("study.in","r",stdin);freopen("study.out","w",stdout); int n;scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&a[i]); long long ans=-1; for(int i=1;i<=n;i++) { for(int j=1;j<=tot;j++)Gcd[j][0]=gcd(Gcd[j][0],a[i]); Gcd[++tot][0]=a[i];Gcd[tot][1]=i;int tot2=0; for(int j=1;j<=tot;j++) if(Gcd[j][0]!=ggcd[tot2][0]) { ggcd[++tot2][0]=Gcd[j][0];ggcd[tot2][1]=Gcd[j][1]; } tot=tot2; for(int j=1;j<=tot2;j++) { Gcd[j][0]=ggcd[j][0];Gcd[j][1]=ggcd[j][1]; ans=max(ans,(long long)Gcd[j][0]*(long long)(i-Gcd[j][1]+1)); } } cout<<ans; return 0; }
