面包人(van)
【题目描述】
小W为了对抗小C的骑士阵,叫来了一车面包人来攻打他。由于小W的后台很硬,他叫来的这一车总共有n个面包人,从1~n编号。但小C很快就摸清了这车面包人的实力,他发现他们的实力跟他们的编号以及编号的因数个数有着千丝万缕的关系。假设τ(x)为x的因数个数,如果对于编号为x的面包人,满足任意编号比他小的面包人y,都有τ(y)<τ(x),那么编号为x的面包人的实力就强于所有编号比他小的面包人,否则他的实力就弱于所有编号比他小的面包人。现在小C希望知道最强的和最弱的面包人的编号。
【输入数据】
输入只有一行,一个正整数n,表示面包人的个数。
【输出数据】
输出只有一行,两个正整数,分别表示最强的和最弱的面包人编号,两个数之间用空格隔开。
【样例输入】
10
【样例输出】
6 10
【数据范围】
对于8%的数据,n<=10;
对于32%的数据,n<=10^5;
另外8%的数据,n为质数;
对于100%的数据,1<=n<=2*10^9。
【样例解释】
1~10的因数个数分别是1,2,2,3,2,4,2,4,3,4。
所以实力排序从弱到强为:10<9<8<7<5<3<1<2<4<6。
最强的面包人为n以内因数最多的数,如果有多个就输出最小的那一个,如果最强的面包人为n,那么最弱的面包人为n-1,否则最弱的面包人为n。
于是,我们可以通过打表处理出n从1~2000000000的每个最强的面包人。但我们发现数组存不下,于是我们注意到这里面重复的面包人很多,于是对于重复的,我们只记一个,于是一共有68个
1,2,4,6,12,24,36,48,60,120,180,240,360,720,840,1260,1680,2520,5040,7560,10080,15120,20160,25200,27720,45360,50400,55440,83160,110880,166320,221760,277200,332640,498960,554400,665280,720720,1081080,1441440,2162160,2882880,3603600,4324320,6486480,7207200,8648640,10810800,14414400,17297280,21621600,32432400,36756720,43243200,61261200,73513440,110270160,122522400,147026880,183783600,245044800,294053760,367567200,551350800,698377680,735134400,1102701600,1396755360
那么,如果n在表里,则最强的面包人为n,那么最弱的面包人为n-1,如果n不在表里,则最强的面包人为在小于n的最大的在表里的数,最弱的面包人为n。
正解:
至于怎么找出因数最多的数,我们尽量往大的构造。
我们把一个数x质因数分解得到:
x=p1^r1*p2^r2*…*pn^rn,
那么τ(x)=(r1+1)*(r2+1)*…*(rn+1)。
所以对于最优答案x的因数分解,必定有:
对于p1<p2<…<pn,r1>r2>…rn。
打表:

#include<iostream> using namespace std; int Max=-1; bool isprime[1000000];int prime[1000000]; int main() { freopen("xxx.txt","w",stdout); int res=0;int tot=0; for(int i=2;i<=50000;i++) { if(!isprime[i]) { prime[++res]=i; for(int j=i*2;j<=50000;j+=i) { isprime[j]=1; } } } for(int i=1;i<=2000000000;i++) { int ans=0; int k=i,x=1,S=0; for(int j=1;j<=res;j++) { S=0; while(k%prime[j]==0) { S++; k=k/prime[j]; } x=x*(S+1); if(!k)break; } if(x>Max)Max=x,cout<<i<<",",tot++; } cout<<endl<<tot; }
计算:

#include<iostream> #include<cstdio> using namespace std; int Math[68]={1,2,4,6,12,24,36,48,60,120,180,240,360,720,840,1260,1680,2520,5040,7560,10080,15120,20160,25200,27720,45360,50400,55440,83160,110880,166320,221760,277200,332640,498960,554400,665280,720720,1081080,1441440,2162160,2882880,3603600,4324320,6486480,7207200,8648640,10810800,14414400,17297280,21621600,32432400,36756720,43243200,61261200,73513440,110270160,122522400,147026880,183783600,245044800,294053760,367567200,551350800,698377680,735134400,1102701600,1396755360}; int main() { freopen("van.in","r",stdin); freopen("van.out","w",stdout); int n;scanf("%d",&n); if(n==1)return 0*printf("1 1"); if(n==2)return 0*printf("2 1"); for(int i=0;i<68;i++) { if(Math[i]==n)return 0*printf("%d %d",Math[i],Math[i]-1); if(i==67||(Math[i+1]>n&&Math[i]<n))return 0*printf("%d %d",Math[i],n); } return 0; }
寻呼机(pager)
【题目描述】
小H和小S现在都居住在B城,B城地图可以看做是一个n*n的网格图,小H住在(1,1),小S住在(n,n)。B城的通讯设施十分发达,每一个格子中都建有一座类型为cij的通讯塔。位于(i,j)的通讯塔对于消息进行处理后只能将消息传输给位于(i+1,j)或(i,j+1)的通讯塔。一天,小H通过传呼机给小S发了一道长度为n-1的消息。所以消息依次会经历n-1道加密、1道中枢处理和n-1道解密,每个格子负责1道处理,所以一共会经过2n-1个格子;根据加密解密原则,每一次解密会解开最后一次未被解密的加密,且该解密类型必须和对应的那一次加密类型相同,具体表现为对应的两个格子类型cij相同。满足以上条件能把信息成功从(1,1)传输到(n,n)的路径,称为合法信息通路。等待回复的时间很漫长,小H端详着B城地图,他希望知道不同的合法信息通路有多少种。
【输入数据】
第一行一个正整数n,表示B城大小。
接下来n行,每行n个整数,表示B城每个格子的类型cij。
【输出数据】
输出一个整数,表示合法信息通路的种数,答案对10^9+7取模。
【样例输入】
3
1 2 3
1 1 2
2 1 1
【样例输出】
4
【数据范围】
对于10%的数据,n<=10;
对于30%的数据,n<=50;
对于50%的数据,n<=100;
另外5%的数据,所有的cij均相等;
另外10%的数据,0<=cij<=1;
对于100%的数据,1<=n<=500,0<=cij<=10^9。
【样例解释】
4条路径:
① (1,1)-(1,2)-(1,3)-(2,3)-(3,3):12321;
② (1,1)-(1,2)-(2,2)-(2,3)-(3,3):12121;
③ (1,1)-(2,1)-(2,2)-(3,2)-(3,3):11111;
④ (1,1)-(2,1)-(3,1)-(3,2)-(3,3):11211。
题意:在n*n网格里从(1,1)走到(n,n)(只能往左走或往下走),计算回文路径。
考虑从红色的对角线把正方形分成两块考虑
我们用dp[i][j][k]表示在对角线(红色)往左数k条斜线(某条蓝色)的第i列到对角线往右数k条斜线的第j列的路径为回文串的方案数
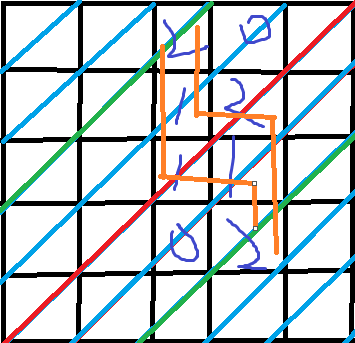
举个例子:dp[3][4][2]=2。即为左上角那个2和右下角那个2(两条绿色斜线的第3列和第4列)之间的组成回文串的路径方案数有2种(橙色)
我们用l表示对角线往左数k条斜线的第i列的所在行,用m表示对角线往右数k条斜线的第j列的所在行。
则l=n+1-i-k,m=n+1-j+k(计算方法为先算出第i列和第j列在红色对角线上的所在行,然后+-k即可)
显然要0<l<=n,0<m<=n,a[l][i]==a[m][j]的时候才更新答案。
dp[i][j][k]=dp[i+1][j-1][k-1]+dp[i][j-1][k-1]+dp[i+1][j][k-1]+dp[i][j][k-1](注意限制条件,i+1<=n,l+1<=n,j-1>0,m-1>0)
但是我们发现会MLE(500*500*500=125000000(内存限制256MB)),又发现转移只和k-1有关,所以我们把k的那一维拿去滚动。
注意:滚动数组使用前要清零(否则还存着上一次的答案)
时间复杂度O(n^3)(但是常数很小)

#include<iostream> #include<cstdio> using namespace std; int dp[511][511][2]; int a[511][511]; const int mod=1e9+7; int main() { freopen("pager.in","r",stdin); freopen("pager.out","w",stdout); int n;scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)scanf("%d",&a[i][j]); for(int i=1;i<=n;i++)dp[i][i][0]=1; for(int k=1;k<n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { int y=k&1;dp[i][j][y]=0;int l=n+1-i-k,m=n+1-j+k; if(l<=0||l>n||m<=0||m>n)continue; if(a[l][i]!=a[m][j])continue; if(i+1<=n&&j-1>0)dp[i][j][y]=(dp[i][j][y]+dp[i+1][j-1][y^1])%mod; if(l+1<=n&&j-1>0)dp[i][j][y]=(dp[i][j][y]+dp[i][j-1][y^1])%mod; if(i+1<=n&&m-1>0)dp[i][j][y]=(dp[i][j][y]+dp[i+1][j][y^1])%mod; if(l+1<=n&&m-1>0)dp[i][j][y]=(dp[i][j][y]+dp[i][j][y^1])%mod; } cout<<dp[1][n][(n-1)&1]; return 0; }
疏散(nuclear)
【题目描述】
没有什么是一颗核弹解决不了的,如果有,那就来两颗。
你的营地现在正在接受小C的核弹轰炸,心灵控制仪矿场啥的估计都要没了。你现在需要紧急疏散你各个建筑物里的部队,你的营地里共有n个建筑,疏散第i个建筑里的部队需要ti的时间,在同一时刻内,你只能疏散一个建筑内的部队。然而你已经通过侦查部队知道了小C对于你的营地的轰炸方案,你的第i个建筑会在si时刻被炸毁,如果一个建筑里的部队正在疏散或还未疏散时建筑被炸毁,那么这个建筑里的部队就不能算被成功疏散,为了能够再积蓄兵力与小C一战,你希望疏散尽量多的建筑里的部队。
【输入数据】
第一行一个正整数n,表示建筑个数。
接下来n行,每行两个整数,ti和si。含义如题中所述。
【输出数据】
输出只有一行,表示最多能疏散多少建筑里的部队。
【样例输入】
3
1 1
10 101
100 101
【样例输出】
2
【数据范围】
对于10%的数据,n<=10;
对于20%的数据,n,ti,si<=2000;
对于50%的数据,n,ti,si<=20000
另外10%的数据,满足所有si都相等。
另外20%的数据,满足所有ti都相等。
对于100%的数据,1<=n<=300000,0<=si,ti<=10^9。
【样例解释】
先疏散第1个建筑,再疏散第2或第3个建筑。
贪心,将每个建筑按摧毁时间从小到大排序。每个建筑能疏散就疏散,不能疏散的就从已经疏散的建筑中找到一个耗时最久的和它比较,如果耗时比它少,就替换之。已经疏散的建筑的耗时可以用一个堆来维护。

#include<iostream> #include<cstdio> #include<algorithm> #include<queue> using namespace std; priority_queue<int>q; struct xxx{ int s,t; }data[300100]; bool cmp(xxx a,xxx b){return a.s<b.s;} int main() { freopen("nuclear.in","r",stdin); freopen("nuclear.out","w",stdout); int n;scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d%d",&data[i].t,&data[i].s); } sort(data+1,data+n+1,cmp); long long Time=0;int ans=0; for(int i=1;i<=n;i++) { if(Time+data[i].t<=data[i].s) { Time+=data[i].t;ans++;q.push(data[i].t); } else if(!q.empty()) { int t2=q.top(); if(data[i].t<t2) { Time=Time-t2+data[i].t; q.pop();q.push(data[i].t); } } } cout<<ans; return 0; }
