1.积木大赛
(block.pas/c/cpp)
【问题描述】
为了庆祝国庆,厦门一中举办了一年一度的“积木大赛”。
在2013年NOIP大赛中,夏夏同学己经搭建了宽度为n的大厦,其中第i块高度为hi。今年比赛的内容是对其NOIP2013搭建大厦进行扩建,使用的材料也都是体积为1正方体积木。
今年搭建的规则是:如果要在某一个位置上放一个积木,必须满足它的左下、下方、右下都有积木(用二维坐标a表示,如果要在a[i,j]位置放积木,那么a[i-1,j-1]、a[i,j-1]、a[i+1,j-1]必须要有积木)。

如果搭的积木大厦越高,夏夏同学就会觉得越有成就感,现有m个积木,问你能搭建的最大高度是多少?
【输入】
第一行两个用空格隔开的整数n和m,分别表示己搭好的宽度和可以使用的积木数量。
后面有n行,每行一个整数hi表示己搭建的第i列积木的高度。
【输出】
一个整数,表示能搭建的最大高度。
【输入输出样例】
|
样例1 |
样例2 |
||
|
block.in |
block.out |
block.in |
block.out |
|
8 4 3 4 2 1 3 3 2 4 |
5 |
3 100 3 3 3 |
4 |
【数据说明】
30%的数据满足:n<=10;m<=1000。
50%的数据满足:n<=100;m<=1000,000。
70%的数据满足:n<=1000;m<=10,000,000。
80%的数据满足:n<=10,000;m<=100,000,000。
100%的数据满足:n<=100,000;m<=1000,000,000;1<=hi<=100000。
二分答案+双指针扫描
二分搭建的高度,最低为maxh+1,最高为maxh+sqrt(m)+1
如何在O(n)时间内check呢?
对于搭建积木,我们要搭出一个金字塔形,但是,并不是要搭建整个金字塔形,有时候只要搭建部分即可,如图:
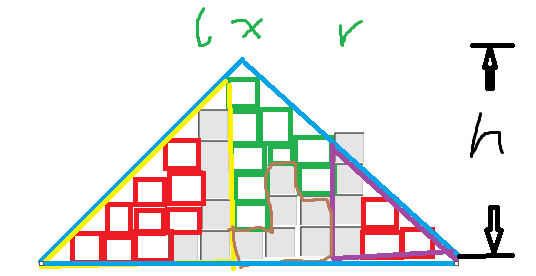
我们仅需搭建绿色部分,而不需要搭建蓝色方框内的整个金字塔
如何找到绿色部分呢?
设l为绿色部分的左边界,r为绿色部分的右边界,x为当前要搭建的金字塔顶,h为大金字塔塔高
我们需要在搭建的金字塔所需积木=整个大金字塔所需积木-黄色部分所需积木-紫色部分所需积木-棕色部分所需积木
设黄色部分高为a,则a=h-(x-l)(即图中6-1=5),黄色部分所需积木为a*(a+1)/2。
同理,能算出紫色部分所需积木。
棕色部分所需积木=r前面所有已有积木-l前面所有已有积木。我们想到了什么?前缀和
这样,绿色部分所需积木就算出来了,我们比较它与m的大小关系即可
等等!还没说l和r怎么求呢?
我们发现,对于一个位置x,如果能找到它所对的l,那么对于位置x-1,它的l必≤位置x所对的l,且从位置x所对的l ~x-1绝对不满足能做绿色部分的左边框。因为在向左移的过程中,左边的每个位置的h的要求总是增大的(金字塔形)
所以l具有单调性。我们从n到1扫描每个位置,如果当前的l不满足h[l]<h-(i-l)(即不能做绿色部分的左边框),那么我们l--,直到满足要求,然后我们拿一个数组记下每个位置的l

对r也是一样,只要从左往右扫描即可。
注意:前缀和要开long long,二分答案的下限一定要从maxh+1开始(不然会引发l==r==i或l>i或r<i等奇奇怪怪的事故),l和r不能小于1或大于n(超出给定范围n外的位置不能放积木)

#include<iostream> #include<cstdio> #include<cmath> using namespace std; typedef long long ll; int h[100001],Max=0; long long bb[100001];int n,m; int L[100001],R[100001]; bool check(int x) { int l=n,r=1; for(int i=n;i>=1;i--){while(h[l]<x-(i-l)&&l>=1)l--;L[i]=l;} for(int i=1;i<=n;i++){while(h[r]<x-(r-i)&&r<=n)r++;R[i]=r;} for(int i=1;i<=n;i++) { if(R[i]==n+1||L[i]==0)continue; int a=x-(i-L[i]),b=x-(R[i]-i); ll y=(ll)x*(ll)x-(ll)(b+1)*(ll)b/2ll-(ll)(a+1)*(ll)a/2ll; if(y-(ll)(bb[R[i]-1]-bb[L[i]])<=(ll)m)return true; } return false; } int main() { // freopen("block.in","r",stdin);freopen("block.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&h[i]);Max=max(Max,h[i]);bb[i]=bb[i-1]+(ll)h[i]; } int l=Max+1,r=(int)(sqrt(m)+1.00)+Max+1; while(l<r) { int mid=(l+r)/2; if(check(mid))l=mid+1; else r=mid; } cout<<l-1; return 0; }
2.爱心月饼
(cake.pas/c/cpp)
【问题描述】
中秋节马上就要到了,电脑组的女生们准备自己动手做月饼给大家分享,烘培老师告诉她们做月饼需要面粉和馅,女孩子们网上各种搜索,采购到了M种面粉和N种口味不同的馅,其中第i种面粉有mi斤,第i种馅有ni斤。这里的种类从0开始标号。
经过实践,女孩子们发现每份月饼需要1斤面粉和1斤馅,为了让收到礼物的同学感到很特别,她们决定不让两份月饼用同一种面粉和同一种馅做成(即每种月饼之间面粉和馅的种类至少有一个不同),女孩子们现在就想知道她们采购到的这些材料可以做多少份爱心月饼?这种简单的问题就交给你啦,她们还得赶着去做月饼呢。
【输入】
由于输入很大,所以使用一种方法生成输入。
l m0= m0
l mi+1 = (mi* 58+md) mod (N + 1)
l n0 = n0
l ni+1 = (ni *58 + nd) mod (M + 1)
第一行6个整数为M,N,m0,md,n0,nd
【输出】
输出一行,为最多能做月饼的份数。
【输入输出样例】
对于10%的操作,N,M ≤ 5.
对于30%的操作,N,M ≤ 1000.
对于50%的操作,N,M ≤ 10 5 .
对于100%的操作,1 ≤ N,M ≤ 2.5 ∗ 10^ 6 , 0 ≤ m0,md ≤ N,0 ≤ n0, nd ≤ M.
【数据说明】
|
cake.in |
cake.out |
|
2 3 1 3 1 0 |
2 |
|
5 8 1 2 3 4 |
19 |
贪心,对于每种面粉,肯定与最大的mi种馅配对。
3.直径
(tree/tree.in/tree.out)
【题目大意】
收到礼物的同学们用爱心月饼摆出了一棵有n个点的树,边有长度。然后得意地给其他同学出了一个问题:对于每一条边,把这条边删掉之后得到的两棵树的直径是多少?
【输入文件】
第一行一个正整数n,表示树的点数
接下来的n-1行每行有三个数u,v,w,表示有一根树枝连接u和v,长度为w
【输出文件】
对于第i条边(从1开始标号),你将会得到2个答案Pi和Qi,我们令ansi=max(Pi,Qi)*23333+min(Pi,Qi)*2333+233*i*i+23*i+2,请输出一个数S表示所有ansi的和对2333333333333333取模的值
【输入样例】
10
1 2 234
2 9 936
9 5 784
5 3 105
2 8 775
8 10 368
10 6 1003
9 4 670
4 7 417
【输出样例】
735923484
【数据规模与约定】
对于10%的数据,保证n≤300
对于30%的数据,保证n≤5000
对于50%的数据,保证n≤100000
对于70%的数据,保证n≤1000000
对于100%的数据,保证n≤4000000,w≤1000000
T3丧病题,下面附上solution和std
10分算法:
对于每条删边在两端O(n^2)求树的直径
时间复杂度O(n^3),空间复杂度O(n)
30分算法:
对于每条删边在两端O(n)求树的直径
时间复杂度O(n^2),空间复杂度O(n)
50分算法:
可以写个点分治冷静一下
要是你真的去写了你就确实应该冷静一下了
时间复杂度O(nlogn),空间复杂度O(n)
100分算法1(不推荐):
树形DP
需要先计算一个点向下走的最大值,次大值,第三大值。
然后计算一个点向上走的最大值。
然后计算这个点和它的父亲的边断掉后这个子树的答案,这个比较好计算。
最后计算这个点和它的父亲的边断掉后这个子树之外的答案,分三种情况:
1、它的父亲的其他儿子的向下答案
2、它的父亲断边之后的答案
3、它的父亲向上的答案
这个做法的细节参见tree2.cpp
注意你不能对每个点扫一遍它的父亲的其它儿子,一个菊花树就能卡掉,要维护一个前缀的最值和一个后缀的最值。
该方法常数可能略大
时间复杂度O(n),空间复杂度O(n)
100分算法2:
先求出树的直径,然后分删掉的边是否在直径上讨论。
删掉的边不在直径上时,其中一端的答案就是直径,另一端做十分简单的树形DP即可。
考虑自左到右计算删掉的边在直径上的左边的答案(右边同理),使用类似NOIP2016day2T2的方法即可。
时间复杂度O(n),空间复杂度O(n)
第二种做法

#include<cstdio> #include<cstring> #include<algorithm> #include<vector> #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define per(i,a,b) for(int i=(a);i>=(b);i--) #define Rep(i,x) for(int i=head[x];i+1;i=nxt[i]) #define pb push_back #include<algorithm> using namespace std; typedef long long ll; const int N=4e6+5; const int M=8e6+5; inline void read(int &x){x=0;char ch=getchar(); while(ch<'0') ch=getchar(); while(ch>='0'){x=x*10+ch-48;ch=getchar();}} inline void judge() { freopen("tree.in","r",stdin); freopen("tree.out","w",stdout); } int fa[N],head[N],nxt[M],to[M],e,w[M],id[M]; int wod[N]; int son[N][2],pd[N],tp[N]; inline void init(){memset(head,-1,sizeof(head)); e=0;} inline void add_edge(int x,int y,int z,int ii){to[e]=y;w[e]=z;nxt[e]=head[x];id[e]=ii;head[x]=e++;} ll ma[N][2],ans[N][2]; inline void Insert(int x,ll y,int cjl,int ii) { if(ma[x][0]<y){ma[x][1]=ma[x][0];ma[x][0]=y;son[x][1]=son[x][0];son[x][0]=cjl;pd[x]=ii;} else if(y>ma[x][1]){ma[x][1]=y;son[x][1]=cjl;} } void dfs(int x) { ma[x][0]=ma[x][1]=0;Rep(i,x) { int j=to[i]; if(j==fa[x]) continue; fa[j]=x; tp[j]=id[i]; dfs(j); Insert(x,ma[j][0]+(ll)w[i],j,tp[j]); } } inline void Insert3(int x,ll y) { if(ma[x][0]<y){ma[x][1]=ma[x][0];ma[x][0]=y;} else if(y>ma[x][1])ma[x][1]=y; } void dfs3(int x,int f,int pp) { ma[x][0]=ma[x][1]=0;ans[pp][0]=0;Rep(i,x) { int j=to[i]; if(j==f) continue; dfs3(j,x,id[i]); Insert3(x,ma[j][0]+(ll)w[i]); ans[pp][0]=max(ans[pp][0],ans[id[i]][0]); }ans[pp][0]=max(ans[pp][0],ma[x][0]+ma[x][1]); } vector<int> tt,Route,Rid,tt2; void dfs2(int x) { tt.push_back(x); if(pd[x])tt2.push_back(pd[x]); if(son[x][0]) dfs2(son[x][0]); else return; } ll md[N]; int main() { judge(); int n;read(n);init();rep(i,1,n-1) { int x,y,z;read(x);read(y);read(z); add_edge(x,y,z,i);add_edge(y,x,z,i); wod[i]=z; }fa[1]=0;dfs(1);int mj=1;rep(i,2,n) if(ma[i][0]+ma[i][1]>ma[mj][0]+ma[mj][1]) mj=i; rep(i,1,n-1) ans[i][1]=ma[mj][0]+ma[mj][1]; if(son[mj][0]) { dfs2(son[mj][0]); for(int i=(int)tt.size()-1;i>=0;i--) Route.pb(tt[i]); for(int i=(int)tt2.size()-1;i>=0;i--) Rid.pb(tt2[i]); tt2.clear();tt.clear(); Rid.pb(tp[son[mj][0]]); } Route.pb(mj); if(son[mj][1]) { Rid.pb(tp[son[mj][1]]); dfs2(son[mj][1]); for(int i=0;i<(int)tt.size();i++) Route.pb(tt[i]); for(int i=0;i<(int)tt2.size();i++) Rid.pb(tt2[i]); } int sz=Route.size();memset(ma,0,sizeof(ma)); ll pre=0;ll maa=0; rep(i,0,sz-1) { int j=Route[i]; Rep(xjt,j) { if(i && to[xjt]==Route[i-1]) continue; if(i<sz-1 && to[xjt]==Route[i+1]) continue; dfs3(to[xjt],j,id[xjt]); md[i]=max(md[i],w[xjt]+ma[to[xjt]][0]); } maa=max(maa,md[i]+pre);if(i!=sz-1)ans[Rid[i]][0]=maa; if(i!=sz-1) pre+=wod[Rid[i]]; } pre=0; maa=0;memset(md,0,sizeof(md)); per(i,sz-1,0) { int j=Route[i]; Rep(xjt,j) { if(i && to[xjt]==Route[i-1]) continue; if(i<sz-1 && to[xjt]==Route[i+1]) continue; dfs3(to[xjt],j,id[xjt]); md[i]=max(md[i],w[xjt]+ma[to[xjt]][0]); } maa=max(maa,md[i]+pre);if(i)ans[Rid[i-1]][1]=maa; if(i) pre+=wod[Rid[i-1]]; } rep(i,1,n-1) if(ans[i][0]>ans[i][1]) swap(ans[i][0],ans[i][1]); ll solo=0; rep(i,1,n-1) { solo+=ans[i][1]*23333ll+ans[i][0]*2333ll+233ll*(ll)i*(ll)i+23ll*(ll)i+2ll; //cerr<<ans[i][1]<<' '<<ans[i][0]<<endl; solo%=2333333333333333ll; } printf("%lld ",solo); return 0; }
第一种做法

#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cstring> #include<vector> using namespace std; inline void read(int &x) { char ch=getchar();x=0; while ((ch<'0')||(ch>'9')) ch=getchar(); while ((ch>='0')&&(ch<='9')) {x=x*10+ch-'0';ch=getchar();} } vector <int> des[4000100],len[4000100]; vector <long long> pre[4000100],suf[4000100]; int s1[4000100],s2[4000100]; int fa[4000100],cop[4000100],wei[4000100]; long long d0[4000100],d1[4000100],d2[4000100],u[4000100],fl[4000100]; int nd0[4000100],nd1[4000100],nd2[4000100]; long long dans[4000100],uans[4000100]; void upd(long long w,int p,int s) { if (w>=d0[s]) { d2[s]=d1[s];nd2[s]=nd1[s]; d1[s]=d0[s];nd1[s]=nd0[s]; d0[s]=w;nd0[s]=p; } else if (w>=d1[s]) { d2[s]=d1[s];nd2[s]=nd1[s]; d1[s]=w;nd1[s]=p; } else if (w>=d2[s]) { d2[s]=w;nd2[s]=p; } } int main() { freopen("cheese.in","r",stdin); freopen("cheese.out","w",stdout); int n;read(n); for (int i=1;i<n;i++) { int u,v,w;read(u);read(v);read(w); s1[i]=u;s2[i]=v; des[u].push_back(v);len[u].push_back(w); des[v].push_back(u);len[v].push_back(w); } int head=1,tail=0;cop[head]=1; while (head!=tail) { int s=cop[++tail]; for (int k=0;k<des[s].size();k++) if (des[s][k]!=fa[s]) { fa[des[s][k]]=s;fl[des[s][k]]=len[s][k];wei[des[s][k]]=k; cop[++head]=des[s][k]; } } for (int i=n;i>=1;i--) { int s=cop[i]; for (int k=0;k<des[s].size();k++) if (des[s][k]!=fa[s]) upd(d0[des[s][k]]+len[s][k],des[s][k],s); } for (int s=1;s<=n;s++) { pre[s].resize(des[s].size()); for (int k=0;k<des[s].size();k++) if (des[s][k]==fa[s]) { if (k) pre[s][k]=pre[s][k-1]; else pre[s][k]=-2100000000; } else { if (k) pre[s][k]=max(pre[s][k-1],d0[des[s][k]]+fl[des[s][k]]); else pre[s][k]=d0[des[s][k]]+fl[des[s][k]]; } suf[s].resize(des[s].size()); for (int k=des[s].size()-1;k>=0;k--) if (des[s][k]==fa[s]) { if (k!=des[s].size()-1) suf[s][k]=suf[s][k+1]; else suf[s][k]=-2100000000; } else { if (k!=des[s].size()-1) suf[s][k]=max(suf[s][k+1],d0[des[s][k]]+fl[des[s][k]]); else suf[s][k]=d0[des[s][k]]+fl[des[s][k]]; } } for (int i=2;i<=n;i++) { int s=cop[i]; if (fa[s]) u[s]=max(u[s],u[fa[s]]+fl[s]); /*for (int k=0;k<des[fa[s]].size();k++) if ((des[fa[s]][k]!=s)&&(des[fa[s]][k]!=fa[fa[s]])) u[s]=max(u[s],d0[des[fa[s]][k]]+fl[des[fa[s]][k]]+fl[s]);*/ if (wei[s]) u[s]=max(u[s],pre[fa[s]][wei[s]-1]+fl[s]); if (wei[s]!=pre[fa[s]].size()-1) u[s]=max(u[s],suf[fa[s]][wei[s]+1]+fl[s]); } for (int i=n;i>=1;i--) { int s=cop[i]; dans[s]=d0[s]+d1[s]; for (int k=0;k<des[s].size();k++) if (des[s][k]!=fa[s]) dans[s]=max(dans[s],dans[des[s][k]]); } for (int s=1;s<=n;s++) { pre[s].resize(des[s].size()); for (int k=0;k<des[s].size();k++) if (des[s][k]==fa[s]) { if (k) pre[s][k]=pre[s][k-1]; else pre[s][k]=-2100000000; } else { if (k) pre[s][k]=max(pre[s][k-1],dans[des[s][k]]); else pre[s][k]=dans[des[s][k]]; } suf[s].resize(des[s].size()); for (int k=des[s].size()-1;k>=0;k--) if (des[s][k]==fa[s]) { if (k!=des[s].size()-1) suf[s][k]=suf[s][k+1]; else suf[s][k]=-2100000000; } else { if (k!=des[s].size()-1) suf[s][k]=max(suf[s][k+1],dans[des[s][k]]); else suf[s][k]=dans[des[s][k]]; } } for (int i=2;i<=n;i++) { int s=cop[i]; uans[s]=uans[fa[s]]; if (nd0[fa[s]]==s) uans[s]=max(uans[s],d1[fa[s]]+max(u[fa[s]],d2[fa[s]])); else if (nd1[fa[s]]==s) uans[s]=max(uans[s],d0[fa[s]]+max(u[fa[s]],d2[fa[s]])); else uans[s]=max(uans[s],d0[fa[s]]+max(u[fa[s]],d1[fa[s]])); /*for (int k=0;k<des[fa[s]].size();k++) if ((des[fa[s]][k]!=fa[fa[s]])&&(des[fa[s]][k]!=s)) uans[s]=max(uans[s],dans[des[fa[s]][k]]);*/ if (wei[s]) uans[s]=max(uans[s],pre[fa[s]][wei[s]-1]); if (wei[s]!=pre[fa[s]].size()-1) uans[s]=max(uans[s],suf[fa[s]][wei[s]+1]); } long long ans=0; for (int i=1;i<n;i++) { if (fa[s2[i]]==s1[i]) swap(s1[i],s2[i]); long long p1=dans[s1[i]],p2=uans[s1[i]]; if (p1<p2) swap(p1,p2); ans+=p1*23333+p2*2333+(long long)i*i*233+(long long)i*23+2; ans%=2333333333333333ll; //cerr<<p1<<' '<<p2<<endl; } printf("%lld ",ans); }
