Mike has a sequence A = [a1, a2, ..., an] of length n. He considers the sequence B = [b1, b2, ..., bn] beautiful if the gcd of all its elements is bigger than 1, i.e. 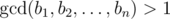 .
.
Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index i (1 ≤ i < n), delete numbers ai, ai + 1 and put numbers ai - ai + 1, ai + ai + 1 in their place instead, in this order. He wants perform as few operations as possible. Find the minimal number of operations to make sequence A beautiful if it's possible, or tell him that it is impossible to do so.
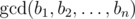 is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).
is the biggest non-negative number d such that d divides bi for every i (1 ≤ i ≤ n).
The first line contains a single integer n (2 ≤ n ≤ 100 000) — length of sequence A.
The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of sequence A.
Output on the first line "YES" (without quotes) if it is possible to make sequence A beautiful by performing operations described above, and "NO" (without quotes) otherwise.
If the answer was "YES", output the minimal number of moves needed to make sequence A beautiful.
2
1 1
YES
1
3
6 2 4
YES
0
2
1 3
YES
1
In the first example you can simply make one move to obtain sequence [0, 2] with 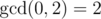 .
.
In the second example the gcd of the sequence is already greater than 1.
题解:我们发现一个位置经过两次操作a[i]变成-2a[i+1],a[i+1]变成2a[i],所以当gcd为1时我们可以把他们都变为偶数,所以我们把所有的数都变为偶数
#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #include<algorithm> using namespace std; const int maxn=1e5+5; int a[maxn],n; int main() { scanf("%d",&n); for(int i=0;i<n;i++) { scanf("%d",&a[i]); } int tmp=a[0]; for(int i=1;i<n;i++) { tmp=__gcd(tmp,a[i]); } if(tmp!=1) { puts("YES\n0"); } else { int ans=0; for(int i=0;i<n;i++) { if(a[i]%2==0)continue; else if(i==n-1) { ans+=2; } else { if(a[i+1]%2!=0)ans++; else ans+=2; i++; } } printf("YES\n%d\n",ans); } }