数字图像处理作业_二维离散快速傅里叶变换_2dfft

笨比来学fft了

先不加推理得给出一维得离散傅里叶变换公式

dft代码实现

def dft(pic_line):#一维离散傅里叶变换暴力n方
    pic_line=np.squeeze(pic_line)
    n=pic_line.size
    w=np.array([[np.exp(-1j*2*np.pi*i*k/n) for k in range(0,n) ] for i in range(0,n)]).T#系数矩阵，生成之后需要转置
    return pic_line.dot(w)

直接这样处理一行像素复杂度为n^2.所以需要快速傅里叶变换

旋转因子具有的性质

推论可以理解为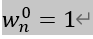的复数在复平面转过半个周期

base=2 FFT算法

由上面算法我们可以知道一个N点dft可以分治为两个N/2的DFT

过程是如下图的蝶形运算式

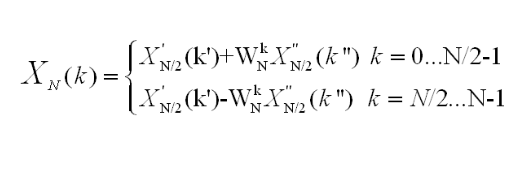
代码实现如下

def Butterfly_operation(seq1,seq2):#蝶形运算 seq1为偶序列，seq2为奇序列
    n=seq1.size
    N=n*2
    seq1=np.squeeze(seq1)#降维
    seq2=np.squeeze(seq2)
    res=np.zeros(2*n,dtype=seq1.dtype)
    for i in range(0,n):
        res[i]+=seq1[i]+np.exp(-1j*2*np.pi*i/N)*seq2[i]
        res[n+i]=seq1[i]-np.exp(-1j*2*np.pi*i/N)*seq2[i]
    return  res

之后我们就可以通过递归分治，或者二进制倒序数实现重排，来实现一维的fft ,时间复杂度为o(nlogn)

从一维得到二维其实很简单，就是先对输入的图像（m×n）的每一行先做一维fft，把结果存到一个（m×n）的矩阵A中，再对矩阵A的每一列做fft。这时得到的结果就是二维图像（m×n）的fft。

实现图像空间域变到频率域通过二维fft算法大妈如下

import numpy as np
import math
import matplotlib.pyplot as plt
from numpy.fft import *
from PIL import Image as IMG
import cv2 as cv
def dft(pic_line):#一维离散傅里叶变换暴力n方
    pic_line=np.squeeze(pic_line)
    n=pic_line.size
    w=np.array([[np.exp(-1j*2*np.pi*i*k/n) for k in range(0,n) ] for i in range(0,n)]).T#系数矩阵，生成之后需要转置
    return pic_line.dot(w)

def Butterfly_operation(seq1,seq2):#蝶形运算 seq1为偶序列，seq2为奇序列
    n=seq1.size
    N=n*2
    seq1=np.squeeze(seq1)#降维
    seq2=np.squeeze(seq2)
    res=np.zeros(2*n,dtype=seq1.dtype)
    for i in range(0,n):
        res[i]+=seq1[i]+np.exp(-1j*2*np.pi*i/N)*seq2[i]
        res[n+i]=seq1[i]-np.exp(-1j*2*np.pi*i/N)*seq2[i]
    return  res

def fft(img):#递归分治实现fft,只对图像的每一行做fft
    n=img.shape[1]
    if(n%2!=0):
        return ValueError("图片大小不是2的次幂")#因为fft分治时每次都分为等大的奇数列和偶数列
    if(n<=8):#n足够小，直接n方对每行求dft
        return np.array([dft(img[i, :]) for i in range(img.shape[0])])
    res_odd=fft(img[:,1::2])
    res_even=fft(img[:,0::2])
    return  np.array([Butterfly_operation(res_even[i:i+1,:],res_odd[i:i+1,:]) for i in range(0,img.shape[0])])

def TwoD_fft(img):
    return fft(fft(img).T).T
def FFT_SHIFT(img):
    M, N = img.shape
    M = int(M / 2)
    N = int(N / 2)
    return np.vstack((np.hstack((img[M:, N:], img[M:, :N])), np.hstack((img[:M, N:], img[:M, :N]))))

if __name__ == '__main__':
    img = cv.imread(r"C:UsersUSERPicturesSaved Pictures	est.jpg", cv.IMREAD_COLOR)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
    gray=gray[0:1024,0:1024]
    fig, ax = plt.subplots(1, 2)
    my_fft = abs(FFT_SHIFT(TwoD_fft(gray)))
    target = abs(fftshift(fft2(gray)))
    plt.subplot(2, 2, 1)
    plt.imshow(gray)
    plt.subplot(2, 2, 2)
    plt.title('FFT2D')
    plt.imshow(np.log(1 + my_fft))
    plt.subplot(2,2,3)
    plt.title('numpy.fft2')
    plt.imshow(np.log(1+target))
    plt.show()
    plt.title('Lenna')

运行结果

参考文献：

数字信号处理--FFT与蝶形算法--学习笔记

十分简明易懂的FFT（快速傅里叶变换）