原文:https://www.cnblogs.com/wanmeishenghuo/p/9495977.html
内容参考: 狄泰软件学院相关教程
常见的时间复杂度如下:

常见的时间复杂度的比较:

实例分析:


从上图的分析中,最坏的情况更具有现实的意义。
当算法在最坏的情况下仍能满足需求时,可以推断,算法的最好情况和平均情况都满足要求。
在数据结构课程中,在没有特殊说明时,所分析算法的时间复杂度都是指最坏时间复杂度。
算法的空间复杂度

空间复杂度示例:
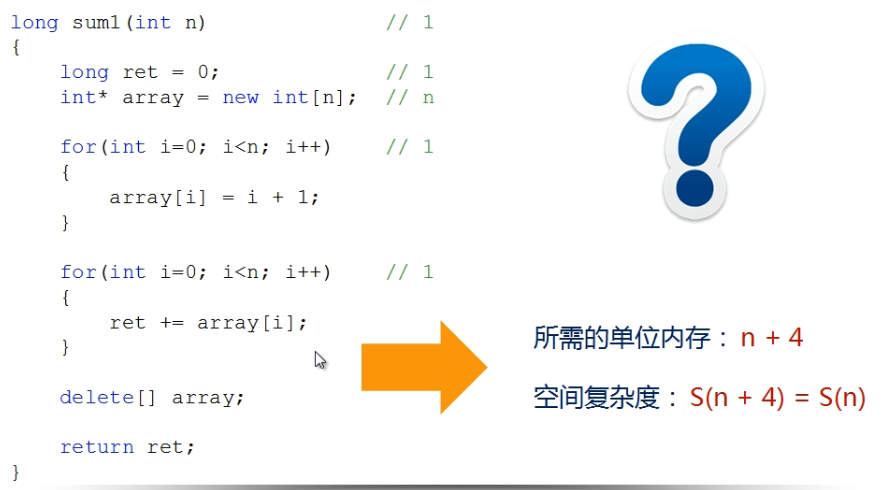
空间与时间的策略:
多数情况下,算法的时间复杂度更令人关注
如果有必要,可以通过增加额外空间降低时间复杂度
同理,也可以增加算法的耗时降低空间复杂度
空间换时间的例子:
/* 问题: 在一个由自然数1-1000中某些数字所组成的数组中,每个数字可能出现零次或者多次。 设计一个算法,找出出现次数最多的数字。 */ #include <iostream> using namespace std; void search(int a[], int len) // O(n) { int sp[1000] = {0}; int max = 0; for(int i=0; i<len; i++) { sp[a[i] - 1]++; } for(int i=0; i<1000; i++) { if( max < sp[i] ) { max = sp[i]; } } for(int i=0; i<1000; i++) { if( max == sp[i] ) { cout << i + 1 << endl; } } } int main(int argc, char* argv[]) { int a[] = {1, 1, 3, 4, 5, 6, 6, 6, 3, 3}; search(a, sizeof(a)/sizeof(*a)); return 0; }
上面的例子中时间复杂度为O(n)。
当两个算法的大O表示法相同时,是否意味着两个算法的效率完全相同呢?
只能说明它们的运行效率时同一个级别的,不能说它们的效率完全相同。
总结:
一般而言,工程中使用的算法,时间复杂度不超过O(n*n*n)。
算法分析与设计时,重点考虑最坏情况下的时间复杂度
数据结构课程中重点关注算法的时间复杂度
大O表示法同样适用于算法的空间复杂度
空间换时间是工程开发中常用的策略