问题 F: 送分题
时间限制: 1 Sec 内存限制: 128 MB
题目描述
给定一棵N个节点的树,每个节点上有一个权值,你要从中选出一些点使得权值和最大,任意2个选出的节点之间的距离都要大于K。
为什么这题要叫送分题呢?
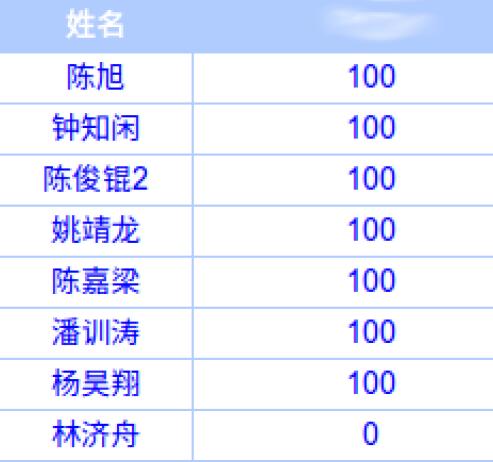
为什么这题要叫送分题呢?

输入
第一行两个整数N,K。
接下来一行N个整数,表示第i个节点的权值
接下来N-1行,每行2个数a,b,表示点a和点b之间有边相连
接下来一行N个整数,表示第i个节点的权值
接下来N-1行,每行2个数a,b,表示点a和点b之间有边相连
输出
输出一行,表示最大的权值和。
样例输入 Copy
3 1
1 1 1
1 2
1 3
样例输出 Copy
2
提示
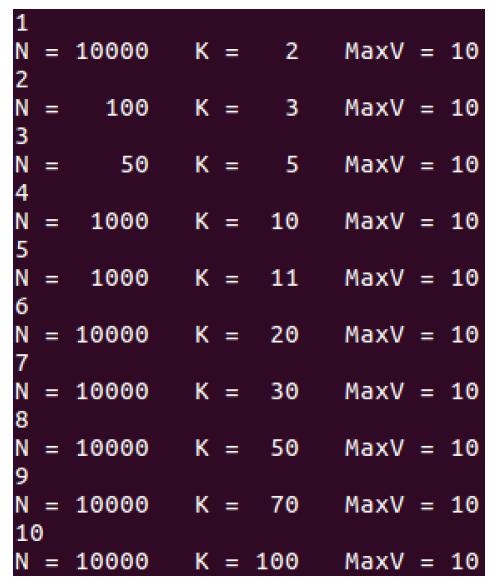
题解:树形DP水题,思路见代码!
AC代码:

1 #pragma GCC optimize(3) 2 #include <bits/stdc++.h> 3 using namespace std; 4 const int maxn=11111; 5 vector<int> edge[maxn]; 6 int v[maxn],n,k,dp[maxn][111]; 7 void dfs(int cur,int fa) 8 { 9 int sum[111]; 10 memset(sum,0,sizeof(sum)); 11 for(int i=0;i<edge[cur].size();i++){ 12 int u=edge[cur][i]; 13 if(u==fa) continue; 14 dfs(u,cur); 15 for(int j=0;j<=k+1;j++){ 16 sum[j]+=dp[u][j]; 17 } 18 } 19 dp[cur][0]=sum[k]+v[cur]; 20 for(int i=1;i<=k+1;i++){ 21 if(i<=(k+1)/2){ 22 for(int j=0;j<edge[cur].size();j++){ 23 int u=edge[cur][j]; 24 if(u==fa) continue; 25 dp[cur][i]=max(dp[cur][i],sum[k+1-i-1]-dp[u][k+1-i-1]+dp[u][i-1]); 26 } 27 } 28 else{ 29 dp[cur][i]=sum[i-1]; 30 } 31 } 32 for(int i=k;i>=0;i--){ 33 dp[cur][i]=max(dp[cur][i],dp[cur][i+1]); 34 } 35 } 36 int main() 37 { 38 scanf("%d %d",&n,&k); 39 for(int i=1;i<=n;i++){ 40 scanf("%d",&v[i]); 41 } 42 for(int i=1;i<=n-1;i++){ 43 int x,y; 44 scanf("%d %d",&x,&y); 45 edge[x].push_back(y); 46 edge[y].push_back(x); 47 } 48 dfs(1,-1); 49 printf("%d ",dp[1][0]); 50 return 0; 51 }
