python 实现简单的感知机

最近在自学机器学习，记录下一些学习记录

如何用python实现一个简单的感知机

需要安装numpy库，即下面用到的np

简单的说就是

通过计算权重向量w和输入向量x的线性组合，判断该线性组合是否大于某个阀值，如果是，输出1，不是，输出-1

根据判断结果与正确结果对比，调整权重向量w，得到最佳的权重向量。从而可以预测新的值属于哪一类

更新权重值的公式

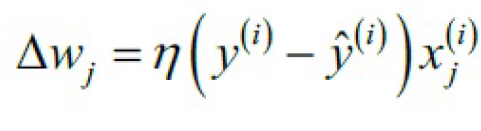
n是学习率值在0.0-1.0之间，yi是正确值，yi^是预测值，xji是x在j点的值

class Perceptron(object):
    """分类感知机.
    参数
    ------------
    eta:float
        学习率 (在 0.0 到 1.0之间)
    n_iter:int
        迭代次数

    属性
    ------------
    w_: ld-array:
        权重
    errors_: list
        误差
    """

    def __init__(self, eta=0.01, n_iter=10):
        self.eta = eta
        self.n_iter = n_iter

    def fit(self, X, y):
        """适应训练集

        参数
        ---------------
        X: array-like, shape=[n_smaples, n_features]
            训练集数组(m*1),  n_samples 是样本数量  n_features 特征值数量
        y: array-like, shape=[n_samples]
            目标值(m*1)

        Returns
        --------------
        self: object
        """
        # 初始化权重函数和误差，权重函数为全一的数组
        self.w_ = np.zeros(1+X.shape[1])# 多了w0
        self.errors_ = []

        for _ in range(self.n_iter):
            errors = 0
            for xi, target in zip(X, y):
                update = self.eta * (target - self.predict(xi))
                self.w_[1:] += update * xi
                self.w_[0] += update # w0 = w0 * x0 = w0 * 1 = w0
                errors += int(update != 0.0)
            self.errors_.append(errors)
        return self

    def net_input(self, X):
        """计算权重w_与X的乘积"""
        return np.dot(X, self.w_[1:]) + self.w_[0]

    def predict(self, X):
        """激活(预测)函数 权重和X的乘积大于0位1否则为-1"""
        return np.where(self.net_input(X) >= 0.0, 1, -1)

 本感知机是基础的感知机，只限用于区分两个线性可分的类别