畅通工程
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 21106 Accepted Submission(s): 10953
Problem Description
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
Input
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是城镇数目N ( < 1000 )和道路数目M;随后的M行对应M条道路,每行给出一对正整数,分别是该条道路直接连通的两个城镇的编号。为简单起见,城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时,输入结束,该用例不被处理。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时,输入结束,该用例不被处理。
Output
对每个测试用例,在1行里输出最少还需要建设的道路数目。
Sample Input
4 2 1 3 4 3 3 3 1 2 1 3 2 3 5 2 1 2 3 5 999 0 0
Sample Output
1 0 2 998
#include<iostream>
#include<cstdio>
#include<map>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<set>
#include<string>
#include<queue>
#include <stack>
using namespace std;
#pragma warning(disable : 4996)
const int MAX = 1005;
int father[MAX];
int ranks[MAX];
int ans;
// 初始化
void Make_Set(int n)
{
for(int i=1; i<=n; ++i)
{
father[i] = i;
ranks[i] = 0;
}
}
// 查找
int Find_Set(int x)
{
if(x != father[x])
return Find_Set(father[x]);
return x;
}
// 合并
void Union_Set(int x, int y)
{
x = Find_Set(x);
y = Find_Set(y);
if(x == y) // x,y在同一个集合
return;
if(ranks[x] > ranks[y])
father[y] = x;
else if(ranks[x] < ranks[y])
father[x] = y;
else
{
ranks[y]++;
father[x] = y;
}
ans--;
}
int main()
{
freopen("in.txt", "r", stdin);
int n, m, x, y;
while (cin >> n)
{
if(n == 0)
{
break;
}
Make_Set(n);
cin >> m;
ans = n;
while (m--)
{
cin >> x >> y;
Union_Set(x, y);
}
cout << ans - 1 << endl;
}
return 0;
}
小希的迷宫
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 17917 Accepted Submission(s): 5466
Problem Description
上次Gardon的迷宫城堡小希玩了很久(见Problem B),现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样,首先她认为所有的通道都应该是双向连通的,就是说如果有一个通道连通了房间A和B,那么既可以通过它从房间A走到房间B,也可以通过它从房间B走到房间A,为了提高难度,小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子,前两个是符合条件的,但是最后一个却有两种方法从5到达8。


Input
输入包含多组数据,每组数据是一个以0 0结尾的整数对列表,表示了一条通道连接的两个房间的编号。房间的编号至少为1,且不超过100000。每两组数据之间有一个空行。
整个文件以两个-1结尾。
整个文件以两个-1结尾。
Output
对于输入的每一组数据,输出仅包括一行。如果该迷宫符合小希的思路,那么输出"Yes",否则输出"No"。
Sample Input
6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1
Sample Output
Yes Yes No#include<iostream> #include<cstdio> #include<map> #include<cstring> #include<cmath> #include<vector> #include<algorithm> #include<set> #include<string> #include<queue> #include <stack> using namespace std; #pragma warning(disable : 4996) const int MAX = 100001; int father[MAX]; int ranks[MAX]; // 初始化 void Make_Set(int n) { for(int i = 1; i <= n; ++i) { father[i] = i; ranks[i] = 0; } } // 查找 int Find_Set(int x) { if(x != father[x]) father[x] = Find_Set(father[x]); return father[x]; } // 合并 void Union_Set(int x, int y) { x = Find_Set(x); y = Find_Set(y); if(x == y) // x,y在同一个集合 return; if(ranks[x] > ranks[y]) { father[y] = x; } else if(ranks[x] < ranks[y]) { father[x] = y; } else { father[x] = y; ranks[x]++; } } int main() { freopen("in.txt", "r", stdin); int n, m; bool flag; while (scanf("%d %d", &n, &m) != EOF) { if(n == -1 && m == -1) { break; } if(n == 0 && m == 0) { printf("Yes\n"); continue; } Make_Set(MAX); ranks[n] = 1; ranks[m] = 1; Union_Set(n, m); flag = true; while (scanf("%d %d", &n, &m) != EOF) { if(n == 0 && m == 0) { break; } ranks[n]++; ranks[m]++; if(Find_Set(n) == Find_Set(m)) { flag = false; } Union_Set(n, m); } int ans = 0; for(int i = 1; i <= MAX; i++) { if(ranks[i] != 0 && i == Find_Set(i)) { ans++; } } if(flag && ans == 1) { printf("Yes\n"); } else { printf("No\n"); } } return 0; }How Many Tables
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 8525 Accepted Submission(s): 4163Problem DescriptionToday is Ignatius' birthday. He invites a lot of friends. Now it's dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.
One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.
For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.InputThe input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.OutputFor each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.Sample Input2 5 3 1 2 2 3 4 5 5 1 2 5Sample Output2 4#include <iostream> using namespace std; int t,m,n,sum,a,b,father[50005]; void MakeSet(int n) { for(int i=1;i<=n;i++) father[i] = i; } int FindSet(int x) { if(x!=father[x]) { father[x] = FindSet(father[x]); } return father[x]; } void UnionSet(int m) { for(int i=1;i<=m;i++) { cin>>a>>b; a = FindSet(a); b = FindSet(b); if(a!=b) { father[a] = b; sum--; } } cout << sum << endl; } int main() { cin>>t; while(t--) { cin>>n>>m; sum = n; MakeSet(n); UnionSet(m); } return 0; }Is It A Tree?
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 9412 Accepted Submission(s): 2201Problem DescriptionA tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
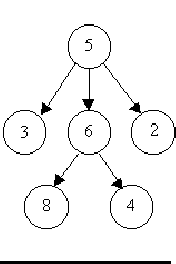
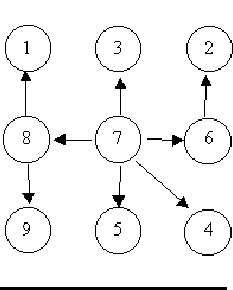
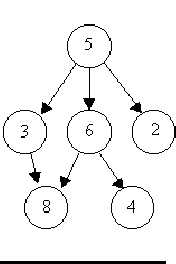
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.InputThe input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.OutputFor each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).Sample Input6 8 5 3 5 2 6 4 5 6 0 0 8 1 7 3 6 2 8 9 7 5 7 4 7 8 7 6 0 0 3 8 6 8 6 4 5 3 5 6 5 2 0 0 -1 -1Sample OutputCase 1 is a tree. Case 2 is a tree. Case 3 is not a tree.POJ,ZOJ都过了,hdoj一直wa,好吧#include <iostream> using namespace std; #define MAX 100005 int father[MAX],ranks[MAX]; void MakeSet(int n) { for(int i=1;i<=n;i++) { father[i] = i; ranks[i] = 0; } } int FindSet(int x) { if(x!=father[x]) father[x] = FindSet(father[x]); return father[x]; } void MergeSet(int x,int y) { x = FindSet(x); y = FindSet(y); if(x==y) return; if(ranks[x]>ranks[y]) father[y] = x; else if(ranks[x]<ranks[y]) father[x] = y; else { ranks[y]++; father[x] = y; } } int main() { freopen("in.txt", "r", stdin); int m,n,count=1; bool check; while(cin>>n>>m) { check = false; if(n < 0 && m < 0) break; if(n == 0 && m == 0) { cout<<"Case "<<count++<<" is a tree."<<endl; continue; } MakeSet(MAX); ranks[n] = 1; ranks[m] = 1; MergeSet(n,m); int flag = 1; if(n == m) { check = true; } while(cin>>n>>m) { if(n == 0 && m == 0) { break; } if(n == m) { check = true; } ranks[n] = 1; ranks[m] = 1; if(FindSet(n)==FindSet(m)) flag = 0; else MergeSet(n,m); } int cnt = 0; for(int i=1;i<=MAX;i++) { if(ranks[i]&&i==FindSet(i)) { cnt++; } } if(flag && cnt == 1 && !check) cout<<"Case "<<count++<<" is a tree."<<endl; else cout<<"Case "<<count++<<" is not a tree."<<endl; } return 0; }