poj_1470Closest Common Ancestors

Closest Common Ancestors

Time Limit: 2000MS		Memory Limit: 10000K
Total Submissions: 12891		Accepted: 4207

Description

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input

The data set, which is read from a the std input, starts with the tree description, in the form: 

nr_of_vertices 
vertex:(nr_of_successors) successor1 successor2 ... successorn 
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form: 
nr_of_pairs 
(u v) (x y) ... 

The input file contents several data sets (at least one). 
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output

For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times 
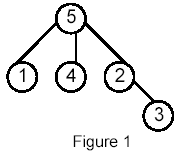
For example, for the following tree: 

Sample Input

5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
      (2 3)
(1 3) (4 3)

Sample Output

2:1
5:5

数据读入好奇葩

#include <iostream>
#include <cstdio>
#include <cstring>
#include <set>
using namespace std;
int main()
{
	int x, y;
	scanf("(%d %d)", &x, &y);
	cout << x << " " << y << endl;
	return 0;
}

这样进行标准输入的时候，不会忽略前导空白字符。。。

#include <iostream>
#include <vector>
#include <cstdio>
#include <cstring>
#include <map>
using namespace std;
#pragma warning(disable : 4996)

const int MAX = 10005;
int father[MAX];//表示x的父节点
int ranks[MAX];//表示x的秩
int indegree[MAX];//保存每个节点的入度
bool visited[MAX];//标记访问
vector<int> tree[MAX], Ques[MAX];
int ancestor[MAX];
map<int, int> ans;

void init(int n)
{
	for(int i = 1; i <= n; i++)
	{

		ranks[i] = 1;
		father[i] = i;
		indegree[i] = 0;
		visited[i] = false;
		ancestor[i] = 0;
		tree[i].clear();
		Ques[i].clear();
	}

}

int find(int x)
{
	if(x != father[x])
	{
		father[x] = find(father[x]);
	}
	return father[x];
}//查找函数，并压缩路径

void Union(int x, int y)
{
	x = find(x);
	y = find(y);
	if(x == y)
	{
		return;
	}
	else if(ranks[x] <= ranks[y])
	{
		father[x] = y;
		ranks[y] += ranks[x];
	}
	else
	{
		father[y] = x;
		ranks[x] += ranks[y];
	}

}//合并函数

void LCA(int u)
{
	ancestor[u] = u;
	for(int i = 0; i < tree[u].size(); i++)
	{
		LCA(tree[u][i]);
		Union(u, tree[u][i]);
		ancestor[find(u)] = u;
	}
	visited[u] = true;
	for(int i = 0; i < Ques[u].size(); i++)
	{
		//如果已经访问了问题节点,就可以返回结果了.
		if(visited[Ques[u][i]])
		{
			//printf("%d\n", ancestor[find(Ques[u][i])]);
			ans[ancestor[find(Ques[u][i])]]++;
			//break;
		}
	}
}

int main()
{
	freopen("in.txt", "r", stdin);
	int n, x, y, t, q;
	while(scanf("%d", &n) != EOF)
	{
		ans.clear();
		init(n);
		for(int i = 1; i <= n; i++)
		{
			scanf("%d:(%d)", &x, &t);
			while (t--)
			{
				scanf("%d", &y);
				tree[x].push_back(y);
				indegree[y]++;
			}
		}
		scanf("%d", &q);
		while (q--)
		{
			while (getchar() != '(')
			{
				;
			}
			scanf("%d %d", &x, &y);
			Ques[x].push_back(y);
			Ques[y].push_back(x);
			while (getchar() != ')')
			{
				;
			}
		}
		for(int i = 1; i <= n; i++)
		{
			//寻找根节点
			if(indegree[i] == 0)
			{
				LCA(i);
				break;
			}
		}
		map<int, int>::iterator it;
		for (it = ans.begin(); it != ans.end(); it++)
		{
			printf("%d:%d\n", it->first, it->second);
		}
	}
	return 0;
}