引言--面试常见的问题
问:“你用过HashMap,你能跟我说说它吗?”
“当然用过,HashMap是一种<key,value>的存储结构,能够快速将key的数据put方式存储起来,然后很快的通过get取出来”,然后说“HashMap不是线程安全的, 答:
HashTable是线程安全的,通过synchronized实现的。HashMap取值非常快”等等。这个时候说明他已经很熟练使用HashMap的工具了。
问:“你知道HashMap 在put和get的时候是怎么工作的吗?”
答:“HashMap是通过key计算出Hash值,然后将这个Hash值映射到对象的引用上,get的时候先计算key的hash值,然后找到对象”。这个时候已经显得不自信了。
问:“HashMap的key为什么一般用字符串比较多,能用其他对象,或者自定义的对象吗?为什么?”
答:“这个没研究过,一般习惯用String。”
问:“你刚才提到HashMap不是线程安全的,你怎么理解线程安全。原理是什么?几种方式避免线程安全的问题。”
答:“线程安全就是多个线程去访问的时候,会对对象造成不是预期的结果,一般要加锁才能线程安全。”
HashMap的面试问题能够考察面试者的线程问题、Java内存模型问题、线程可见与不可变问题、Hash计算问题、链表结构问题、二进制的&、|、<<、>>等问题。所以一个HashMap就能考验一个人的技术功底了。
一、数据结构
HashMap是数组+链表+红黑树(JDK1.8增加了红黑树部分)实现的,如下图所示
// Node<K,V> 类用来实现数组及链表的数据结构
static class Node<K,V> implements Map.Entry<K,V> {
final int hash; //保存节点的 hash 值
final K key; //保存节点的 key 值
V value; //保存节点的 value 值
Node<K,V> next; //指向链表结构下的当前节点的 next 节点,红黑树 TreeNode 节点中也有用到
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { }
public final V getValue() { }
public final String toString() { }
public final int hashCode() { }
public final V setValue(V newValue) { }
public final boolean equals(Object o) { }
}
public class LinkedHashMap<K,V> {
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
}
// TreeNode<K,V> 继承 LinkedHashMap.Entry<K,V>,用来实现红黑树相关的存储结构
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // 存储当前节点的父节点
TreeNode<K,V> left; //存储当前节点的左孩子
TreeNode<K,V> right; //存储当前节点的右孩子
TreeNode<K,V> prev; // 存储当前节点的前一个节点
boolean red; // 存储当前节点的颜色(红、黑)
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
final TreeNode<K,V> root() { }
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) { }
final TreeNode<K,V> find(int h, Object k, Class<?> kc) { }
final void treeify(Node<K,V>[] tab) { }
final Node<K,V> untreeify(HashMap<K,V> map) { }
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) { }
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab, boolean movable) { }
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) { }
/* ------------------------------------------------------------ */
// Red-black tree methods, all adapted from CLR
// 红黑树相关操作
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,TreeNode<K,V> p) {}
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,TreeNode<K,V> p) { }
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) {}
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,TreeNode<K,V> x) {}
static <K,V> boolean checkInvariants(TreeNode<K,V> t) {}
}
二、成员属性
//创建 HashMap 时未指定初始容量情况下的默认容量
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
//HashMap 的最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
//HashMap 默认的装载因子,当 HashMap 中元素数量超过 容量*装载因子 时,进行 resize() 操作
static final float DEFAULT_LOAD_FACTOR = 0.75f;
//用来确定何时将解决 hash 冲突的链表转变为红黑树
static final int TREEIFY_THRESHOLD = 8;
// 用来确定何时将解决 hash 冲突的红黑树转变为链表
static final int UNTREEIFY_THRESHOLD = 6;
/* 当需要将解决 hash 冲突的链表转变为红黑树时,需要判断下此时数组容量,若是由于数组容量太小(小于 MIN_TREEIFY_CAPACITY )导致的 hash 冲突太多,则不进行链表转变为红黑树操作,转为利用 resize() 函数对 hashMap 扩容 */
static final int MIN_TREEIFY_CAPACITY = 64;
//保存Node<K,V>节点的数组
transient Node<K,V>[] table;
//由 hashMap 中 Node<K,V> 节点构成的 set
transient Set<Map.Entry<K,V>> entrySet;
//记录 hashMap 当前存储的元素的数量
transient int size;
//记录 hashMap 发生结构性变化的次数(注意 value 的覆盖不属于结构性变化)
transient int modCount;
//threshold的值应等于 table.length * loadFactor, size 超过这个值时进行 resize()扩容
int threshold;
//记录 hashMap 装载因子
final float loadFactor;
1、loadFactor参数
如果内存富余,那么建议把loadFactor设置的小一点,但是要注意初始size的设置,如果不合适会导致频繁的 resize 严重影响插入的效率。
如果内存比较吃紧,就可以把loadFactor设置的大一些,但是loadFactor设置大的话,键值对以链表的形式存储的概率就提高,平均的查询时间变慢,但是对于插入而言,虽然没有直接的影响,但是loadFactor提高,
三、构造方法
//构造方法1,指定初始容量及装载因子
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
/* tableSizeFor(initialCapacity) 方法返回的值是最接近 initialCapacity 的2的幂,若指定初始容量为9,则实际 hashMap 容量为16*/
//注意此种方法创建的 hashMap 初始容量的值存在 threshold 中
this.threshold = tableSizeFor(initialCapacity);
}
//tableSizeFor(initialCapacity) 方法返回的值是最接近 initialCapacity 的2的幂
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;// >>> 代表无符号右移
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
//构造方法2,仅指定初始容量,装载因子的值采用默认的 0.75
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
//构造方法3,所有参数均采用默认值
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
四、put方法
当我们往HashMap中put元素的时候,先根据key的hashCode重新计算hash值,根据hash值得到这个元素在数组中的位置(即下标),如果数组该位置上已经存放有其他元素了,那么在这个位置上的元素将以链表的形式存放,新加入的放在链头,最先加入的放在链尾,数组中存储的是最后插入的元素 。如果数组该位置上没有元素,就直接将该元素放到此数组中的该位置上。
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, //这里onlyIfAbsent表示只有在该key对应原来的value为null的时候才插入,也就是说如果value之前存在了,就不会被新put的元素覆盖。
boolean evict) { //evict参数用于LinkedHashMap中的尾部操作,这里没有实际意义。
Node<K,V>[] tab; Node<K,V> p; int n, i; //定义变量tab是将要操作的Node数组引用,p表示tab上的某Node节点,n为tab的长度,i为tab的下标。
if ((tab = table) == null || (n = tab.length) == 0) //判断当table为null或者tab的长度为0时,即table尚未初始化,此时通过resize()方法得到初始化的table。
n = (tab = resize()).length; //这种情况是可能发生的,HashMap的注释中提到:The table, initialized on first use, and resized as necessary。
if ((p = tab[i = (n - 1) & hash]) == null) //此处通过(n - 1) & hash 计算出的值作为tab的下标i,并另p表示tab[i],也就是该链表第一个节点的位置。并判断p是否为null。
tab[i] = newNode(hash, key, value, null); //当p为null时,表明tab[i]上没有任何元素,那么接下来就new第一个Node节点,调用newNode方法返回新节点赋值给tab[i]。
else { //下面进入p不为null的情况,有三种情况:p为链表节点;p为红黑树节点;p是链表节点但长度为临界长度TREEIFY_THRESHOLD,再插入任何元素就要变成红黑树了。
Node<K,V> e; K k; //定义e引用即将插入的Node节点,并且下文可以看出 k = p.key。
if (p.hash == hash && //HashMap中判断key相同的条件是key的hash相同,并且符合equals方法。这里判断了p.key是否和插入的key相等,如果相等,则将p的引用赋给e。
((k = p.key) == key || (key != null && key.equals(k)))) //这一步的判断其实是属于一种特殊情况,即HashMap中已经存在了key,于是插入操作就不需要了,只要把原来的value覆盖就可以了。
e = p; //这里为什么要把p赋值给e,而不是直接覆盖原值呢?答案很简单,现在我们只判断了第一个节点,后面还可能出现key相同,所以需要在最后一并处理。
else if (p instanceof TreeNode) //现在开始了第一种情况,p是红黑树节点,那么肯定插入后仍然是红黑树节点,所以我们直接强制转型p后调用TreeNode.putTreeVal方法,返回的引用赋给e。
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); //你可能好奇,这里怎么不遍历tree看看有没有key相同的节点呢?其实,putTreeVal内部进行了遍历,存在相同hash时返回被覆盖的TreeNode,否则返回null。
else { //接下里就是p为链表节点的情形,也就是上述说的另外两类情况:插入后还是链表/插入后转红黑树。另外,上行转型代码也说明了TreeNode是Node的一个子类。
for (int binCount = 0; ; ++binCount) { //我们需要一个计数器来计算当前链表的元素个数,并遍历链表,binCount就是这个计数器。
if ((e = p.next) == null) { //遍历过程中当发现p.next为null时,说明链表到头了,直接在p的后面插入新的链表节点,即把新节点的引用赋给p.next,插入操作就完成了。注意此时e赋给p。
p.next = newNode(hash, key, value, null); //最后一个参数为新节点的next,这里传入null,保证了新节点继续为该链表的末端。
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st //插入成功后,要判断是否需要转换为红黑树,因为插入后链表长度加1,而binCount并不包含新节点,所以判断时要将临界阈值减1。
treeifyBin(tab, hash); //当新长度满足转换条件时,调用treeifyBin方法,将该链表转换为红黑树。
break; //当然如果不满足转换条件,那么插入数据后结构也无需变动,所有插入操作也到此结束了,break退出即可。
}
if (e.hash == hash && //在遍历链表的过程中,我之前提到了,有可能遍历到与插入的key相同的节点,此时只要将这个节点引用赋值给e,最后通过e去把新的value覆盖掉就可以了。
((k = e.key) == key || (key != null && key.equals(k)))) //老样子判断当前遍历的节点的key是否相同。
break; //找到了相同key的节点,那么插入操作也不需要了,直接break退出循环进行最后的value覆盖操作。
p = e; //在第21行我提到过,e是当前遍历的节点p的下一个节点,p = e 就是依次遍历链表的核心语句。每次循环时p都是下一个node节点。
}
}
if (e != null) { // existing mapping for key //左边注释为jdk自带注释,说的很明白了,针对已经存在key的情况做处理。
V oldValue = e.value; //定义oldValue,即原存在的节点e的value值。
if (!onlyIfAbsent || oldValue == null) //前面提到,onlyIfAbsent表示存在key相同时不做覆盖处理,这里作为判断条件,可以看出当onlyIfAbsent为false或者oldValue为null时,进行覆盖操作。
e.value = value; //覆盖操作,将原节点e上的value设置为插入的新value。
afterNodeAccess(e); //这个函数在hashmap中没有任何操作,是个空函数,他存在主要是为了linkedHashMap的一些后续处理工作。
return oldValue; //这里很有意思,他返回的是被覆盖的oldValue。我们在使用put方法时很少用他的返回值,甚至忘了它的存在,这里我们知道,他返回的是被覆盖的oldValue。
}
}
++modCount; //收尾工作,值得一提的是,对key相同而覆盖oldValue的情况,在前面已经return,不会执行这里,所以那一类情况不算数据结构变化,并不改变modCount值。
if (++size > threshold) //同理,覆盖oldValue时显然没有新元素添加,除此之外都新增了一个元素,这里++size并与threshold判断是否达到了扩容标准。
resize(); //当HashMap中存在的node节点大于threshold时,hashmap进行扩容。
afterNodeInsertion(evict); //这里与前面的afterNodeAccess同理,是用于linkedHashMap的尾部操作,HashMap中并无实际意义。1
return null; //最终,对于真正进行插入元素的情况,put函数一律返回null。
}
①.判断键值对数组table[i]是否为空或为null,否则执行resize()进行扩容;
②.根据键值key计算hash值得到插入的数组索引i,如果table[i]==null,直接新建节点添加,转向⑥,如果table[i]不为空,转向③;
③.判断table[i]的首个元素是否和key一样,如果相同直接覆盖value,否则转向④,这里的相同指的是hashCode以及equals;
④.判断table[i] 是否为treeNode,即table[i] 是否是红黑树,如果是红黑树,则直接在树中插入键值对,否则转向⑤;
⑤.遍历table[i],判断链表长度是否大于8,大于8的话把链表转换为红黑树,在红黑树中执行插入操作,否则进行链表的插入操作;遍历过程中若发现key已经存在直接覆盖value即可;
⑥.插入成功后,判断实际存在的键值对数量size是否超多了最大容量threshold,如果超过,进行扩容。
resize方法
// Initializes or doubles table size,两倍扩容并初始化table
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0; // 新容量,新阀值
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab; //到达极限,无法扩容
}
else if((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold阀值
}
// oldCap=0 ,oldThr>0,threshold(新的扩容resize临界值)
else if (oldThr > 0)
newCap = oldThr; //新容量=旧阀值(扩容临界值)
else { // oldCap=0 ,oldThr=0,调用默认值来初始化
newCap = DEFAULT_INITIAL_CAPACITY;
newThr=(int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr== 0) { //新阀值为0,则需要计算新的阀值
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?(int)ft : Integer.MAX_VALUE);
}
threshold = newThr; //设置新的阀值
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; //创建新的桶
table = newTab;
// table初始化,bucket copy到新bucket,分链表和红黑树
if (oldTab != null) { // 不为空则挨个copy,影响效率!!!
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) { //先赋值再判断
oldTab[j] = null; //置null,主动GC
//如果该桶只有一个元素,重新计算桶位,则直接赋到新的桶里面
if (e.next == null)
//1.6的indexFor,计算key;tableSizeFor性能优化
newTab[e.hash &(newCap - 1)]= e; //hash&(length-1)
else if (e instanceof TreeNode) // 红黑树
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { //链表,preserve order保持顺序
//一个桶中有多个元素,遍历将它们移到新的bucket或原bucket
Node<K,V> loHead = null,loTail = null;//lo原bucket的链表指针
Node<K,V> hiHead = null, hiTail = null;//hi新bucket的链表指针
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {//还放在原来的桶
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e; //更新尾指针
}
else {//放在新桶
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null); //
if (loTail != null) { //原bucket位置的尾指针不为空(即还有node)
loTail.next = null; //链表最后得有个null
newTab[j] = loHead;//链表头指针放在新桶的相同下标(j)处
}
if (hiTail != null) { //放在桶 j+oldCap
hiTail.next = null;
newTab[j + oldCap] = hiHead;//j+oldCap见下
}
}
}
}
}
return newTab;
}
treeifyBin方法
// 转化为树节点
final void treeifyBin(Node<K,V>[] tab, int hash) {
/*int n, index; Node<K,V> e;
// 如果hash为空,或者键值对总数不够,则扩容
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
// 加入的node不为空
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
// 该循环把原本的单向链表,改成使用红黑树节点链接的双向链表
do {
// 单向链表节点转化为红黑树节点
TreeNode<K,V> p = replacementTreeNode(e, null);
// 此处类似构造一个双向链表
if (tl == null)
// hd为头节点
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
// 遍历单向链表
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);
}*/
}
五、get方法
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value; //根据key及其hash值查询node节点,如果存在,则返回该节点的value值。
}
final Node<K,V> getNode(int hash, Object key) { //根据key搜索节点的方法。记住判断key相等的条件:hash值相同 并且 符合equals方法。
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 && //根据输入的hash值,可以直接计算出对应的下标(n - 1)& hash,缩小查询范围,如果存在结果,则必定在table的这个位置上。
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k)))) //判断第一个存在的节点的key是否和查询的key相等。如果相等,直接返回该节点。
return first;
if ((e = first.next) != null) { //遍历该链表/红黑树直到next为null。
if (first instanceof TreeNode) //当这个table节点上存储的是红黑树结构时,在根节点first上调用getTreeNode方法,在内部遍历红黑树节点,查看是否有匹配的TreeNode。
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash && //当这个table节点上存储的是链表结构时,用跟第11行同样的方式去判断key是否相同。
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null); //如果key不同,一直遍历下去直到链表尽头,e.next == null。
}
}
return null;
}
final TreeNode<K,V> getTreeNode(int h, Object k) {
//从根节点开始,调用 find 方法进行查找
return ((parent != null) ? root() : this).find(h, k, null);
}
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
//首先进行hash 值的比较,若不同令当前节点变为它的左孩子或者右孩子
if ((ph = p.hash) > h)
p = pl;
else if (ph < h)
p = pr;
//hash 值相同,进行 key 值的比较
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if (pl == null)
p = pr;
else if (pr == null)
p = pl;
//执行到这儿,意味着hash 值相同,key 值不同
//若k 是可比较的并且k.compareTo(pk) 返回结果不为0可进入下面elseif
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
/*若 k 是不可比较的 或者 k.compareTo(pk) 返回结果为0则在整棵树中进行查找,先找右子树,右子树没有再找左子树*/
else if ((q = pr.find(h, k, kc)) != null)
return q;
else
p = pl;
} while (p != null);
return null;
}
六、remove方法
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
// 与get的逻辑一样
Node<K,V>[] tab; Node<K,V> p; int n, index;
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
else {
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
// 移除逻辑
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// 树的情况
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
else if (node == p)
// 桶中的第一个元素
tab[index] = node.next;
else
// 不是第一个元素
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
七、源码总结
源码分析是一种临界知识,掌握了这种临界知识,能不变应万变,源码分析对于很多人来说很枯燥,生涩难懂。
源码阅读,我觉得最核心有三点:技术基础+强烈的求知欲+耐心。
我认为是阅读源码的最核心驱动力。我见到绝大多数程序员,对学习的态度,基本上就是这几个层次(很偏激哦):
-
只关注项目本身,不懂就baidu一下。
-
除了做好项目,还会阅读和项目有关的技术书籍,看wikipedia。
-
除了阅读和项目相关的书外,还会阅读IT行业的书,比如学Java时,还会去了解函数语言,如LISP。
-
找一些开源项目看看,大量试用第三方框架,还会写写demo。
-
阅读基础框架、J2EE规范、Debug服务器内核。
大多数程序都是第1种,到第5种不光需要浓厚的兴趣,还需要勇气:我能读懂吗?其实,你能够读懂的。
耐心,真的很重要。因为你极少看到阅读源码的指导性文章或书籍,也没有人要求或建议你读。你读的过程中经常会卡住,而一卡主可能就陷进了迷宫。这时,你需要做的,可能是暂时中断一下,再从外围看看它:如API结构、框架的设计图。
下图是我总结出来的目前最应该学习的源码知识点:
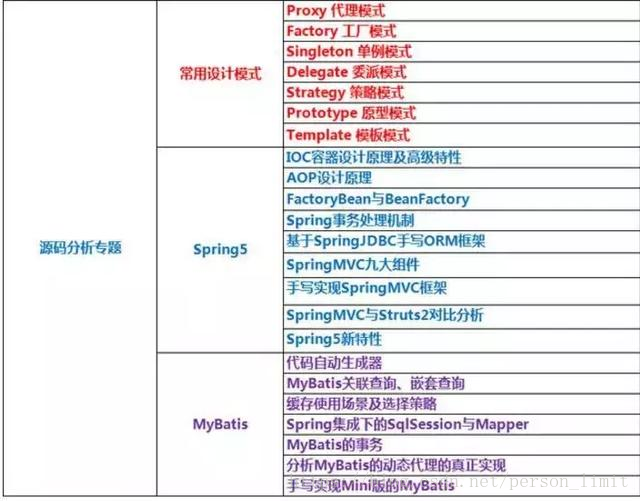
在这里顺便给大家推荐一个交流学习群:650385180,里面会分享一些资深架构师录制的视频录像:有Spring,MyBatis,Netty源码分析,高并发、高性能、分布式、微服务架构的原理,JVM性能优化这些成为架构师必备的知识体系。还能领取免费的学习资源,目前受益良多,相信对于已经工作和遇到技术瓶颈的码友,在这个群里一定有你需要的内容。
参考文献:
http://www.cnblogs.com/jzb-blog/p/6637823.html
https://www.cnblogs.com/wuhuangdi/p/4175991.html
https://www.cnblogs.com/Michaelwjw/p/6411176.html
https://blog.csdn.net/u013140391/article/details/72066906