顶点支配、独立与覆盖

支配集

概念

支配集：设G=(V,E)是无向简单图，D⊆V，若任意v∈V-D,都存在u∈D,使得uv∈E,则称D为一个支配集。

极小支配集：若D是图G的支配集，且D的任何真子集都不再是支配集，则称D为一个极小支配集。

最小支配集：如果图G的支配集D满足对于G的任何支配集D’，都有|D|≤|D’|,则称D是G的一个最小支配集。

支配数：最小支配集D的元素数称为图G的支配数,记作γ(G)。

 例如：

(1)V1、V2、V3不是支配集——>都不与V5相邻

(2)V5、V6、V7构成支配集——>与剩余点都相邻，但不是极小支配集，因为移去V5仍是支配集

(3)V1、V3、V5是极小支配集但不是最小支配集——>由(2)知最小支配集可只包含两个顶点

(4)V6、V3既是极小支配集又是最小支配集

(5)V6、V7也是最小支配集

性质

1、对于V中任意一个顶点而言，它或者属于支配集，或者与支配集中的一个元素相邻

2、一个图中极小支配集可能不唯一

3、一个图中最小支配集可能不唯一

4、最小支配集一定是极小支配集，但极小支配集不一定是最小支配集

5、特殊图中的支配集

(a)在任意简单图G=(V,E),V都是支配集

(b)完全图K_n(n≥3)的支配数为1

(c)完全二分图K_n,m 的支配数为min(n,m)

实例

例如，在一个分布式计算系统中，每个节点都有一台计算服务器，有些节点放置数据存储器，节点之间使用数据线连接。为了提高访问速度，要求每个节点都可以直接访问数据存储器，同时为了节约成本要求数据存储器尽可能少，该如何放置？

选择最小支配集放置数据储存器。

点独立集

概念

独立集：设G=(V,E)是一个无向图，S⊆V，若对任意地u,v∈S,都有u,v不相邻，则S是G的点独立集或简称独立集。

极大独立集：若对G的任意独立集T，都有S⊄T，则称S是G的一个极大独立集

最大独立集：称基数最大的独立集为最大独立集

独立数：图G中最大独立数的基数称为独立数，记作α(G)

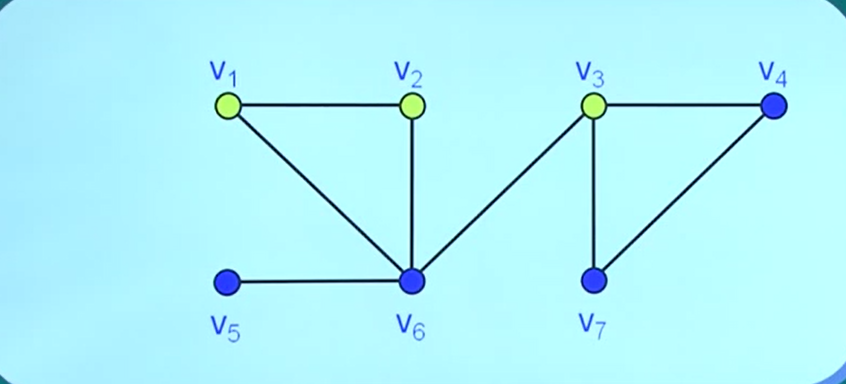
(1)V1、V2、V3不是独立集——>V1、V2相邻

(2)V1、V3是独立集但不是极大独立集——>还可以向其中添加顶点V5

(3)V4、V6是极大独立集但不是最大独立集——>由(2)知顶点数可为3

(4)V1、V3、V5既是极大独立集也是最大独立集

性质

1、极大独立集不是任何其它独立集的子集

2、若S是G的极大独立集，则对任意u∈V-S，都存在v∈S，使得u,vv相邻

3、一个图的极大独立集可能不唯一

4、一个图的最大独立集可能不唯一

5、最大独立集一定是极大独立集，极大独立集不一定是最大独立集

6、特殊图中的独立集

(a)在任意图中，空集都是独立集

(b)完全图K_n(n≥3)的独立数为1

(c)完全二分图K_n,m 的独立数为max(n,m)

7、独立数和支配数之间的关系：

定理1：一个独立集也是支配集当且仅当它是极大独立集。

定理2：简单无向图的极大独立集也是极小支配集

实例

在某个通讯系统中，由于电磁干扰，输入符号可能和输出符号不同

因此该通讯系统中只能使用{a_1,a_2,a_3,a_4,a₅}中的部分符号，而不是全体。例如可以使用a₁,a₄,不能使用a_1,a₃,因为输出是a₁时将无法区分。

但又从效率角度出发，希望能提供使用的符号尽可能地多。

 

如果符号x,y具有相同的输出，则在顶点x,y之间连一条边。如图

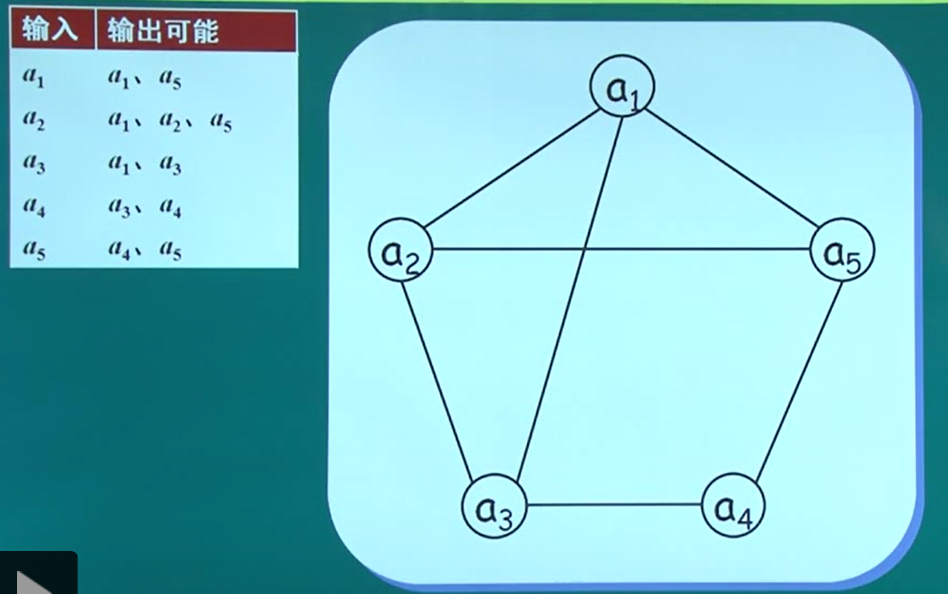
寻找最大独立集a₁,a₄，就是我们能使用的符号（或a₂,a₄）

点覆盖集

概念

点覆盖：设G=(V,E),V’⊆V,如果对任意的e∈E,都存在v∈V’，使得v是e的一个端点，则称V’是G的一个点覆盖集，简称点覆盖。

极小点覆盖：如果V* 是点覆盖，且V*的任何真子集都不再是点覆盖，则称V*是极小点覆盖

最小点覆盖：基数最小的点覆盖称作最小点覆盖

点覆盖数：最小点覆盖V*的基数称作图G的点覆盖数β(G)

(1)V1、V2、V3不是点覆盖——>V5,V6这条边的两个顶点都未被包括

(2)V1、V2、V6、V4、V6、V7是点覆盖但不是极小点覆盖——>可将V2移去

(3)V1、V2、V3、V5、V7是极小点覆盖但不是最小点覆盖

 (4)V1、V3、V4、V6既是极小点覆盖也是最小点覆盖

性质

1、在极小点覆盖中，不存在所有相邻顶点都在V*中的顶点

2、一个图的极小点覆盖可能不唯一

3、一个图的最小点覆盖可能不唯一

4、最大点覆盖一定是极小点覆盖，极小点覆盖不一定是最小点覆盖

5、明显有β(G)≥γ(G)

6、特殊图中的点覆盖

(a)在任一简单图中，V都是点覆盖

(b)完全图K_n(n≥3)的点覆盖数为n - 1

(c)完全二分图K_n,m 的独立数为min(n,m)

7、点覆盖集与点独立集之间的关系：

定理一：在简单图G=(V,E)中，V*⊆V是点覆盖集当且仅当V-V*是独立集

推论一：在简单图G=(V,E)中，V*⊆V是极小点覆盖集当且仅当V-V*是极大独立集

 推论二：在简单图G=(V,E)中，V*⊆V是最小点覆盖集当且仅当V-V*是最大独立集，继而有α(G) + β(G) = |V|

参考链接：中国大学mooc 离散数学 刘铎