概念
分块算法实质上是一种是通过分成多块后在每块上打标记以实现快速区间修改，区间查询的一种算法。其均摊时间复杂度为 $O(sqrt n)$
分块的基本思想是通过适当的划分，预处理一部分信息并保存下来，用空间换取时间，达到时空平衡。事实上，分块更接近于“朴素”，效率往往比不上树状数组和线段树，但是它更加通用、容易实现。
大部分常见的分块思想都可以用“大段维护、局部朴素”来形容。
基本操作及性质
我们经常讲一个长度为 n 的序列分为 $sqrt n$ 个大小为 $sqrt n$ 的块，如果不是完全平方数，则序列最右端会多出一个角块。如图，就是一种序列的分块：
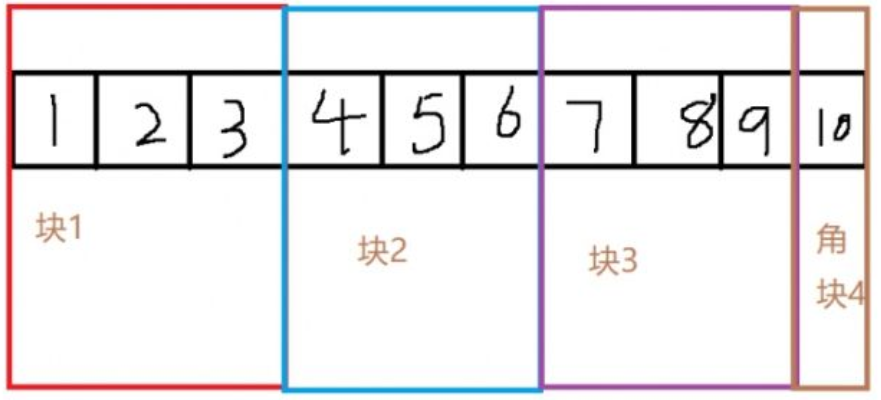
获取一个序号的所在块可通过如下代码：
int n;//总个数 int size=sqrt(n);//每一块大小 for(int i=1;i<=n;i++) { block[i]=(i-1)/size+1;//每一个数所在块 }
区间修改和区间查询都是：对整段的修改/查询标记，对于不是整段的采取朴素算法，因为段树和段长都是 $O(sqrt N)$，所以单次操作的复杂度是 $O(sqrt N)$，整个算法的复杂度是 $O((N + Q)* sqrt NN)$.
分块的实质
分块其实是一种树形结构，它是一种只有三层的树，形态如下：
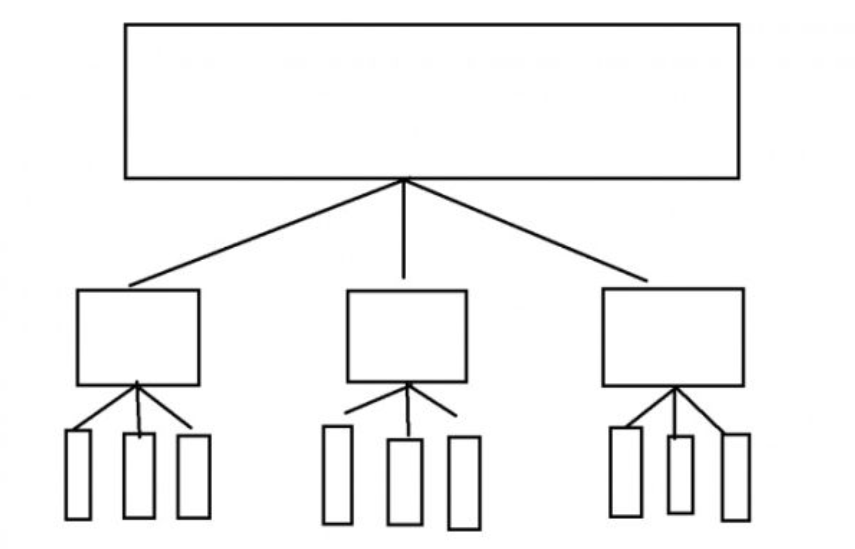
分块算法的延伸
- 莫队
莫队算法的思路是，离线情况下对所有的询问进行一个 sort() ，然后两个指针 l,r（本题是两个，其他的题可能会更多不断以看似暴力的方式在区间内跳来跳去，最终输出答案。 掌握一个思想基础：两个询问之间的状态跳转。
如图，当前完成的询问的区间为 [a,b]] ,下一个询问的区间为 [p,q] ,现在保存 [a,b] 区间内的每个颜色出现次数的 sum[] 数组已经准备好， [a,b] 区间询问的答案 Ans1 已经准备好，怎样用这些条件求出 [p,q] 区间询问的 Ans2？
方法是：通过分块加速，使得莫队的时间复杂度均摊为 $O(n sqrt n)$
- 带修莫队
带修莫队，是建立在莫队基础上的一种算法。当原序列受到影响时，莫队中存储的答案必定会改变，那么我们如何避免修改操作带来的影响呢？
首先，我们需要将查询操作和修改操作分别记录下来。
在记录查询操作的时候，需要增加一个变量来记录离本次查询最近的修改的位置，你需要一个变量记录现在已经做了几次修改。如果改多了，你就要改回去，所以可以得到带修改的莫队分为三维，左指针，右指针，以及当前修改次数。和普通莫队一样，我们先对所有操作 sort 一遍后，每次再查询。