大组合数取模——卢卡斯定理

我们学了O(n^2)的做法，加上逆元，我们又会了O(n)的做法，

在来了新问题，如果n和m很大呢，

比如求C(n, m) % p  ， n<=1e18,m<=1e18,p<=1e5

看到没有，n和m这么大，但是p却很小，我们要利用这个p。

接下来进入正题： 
Lucas定理针对该取值范围较大又不特别大的情况

定理描述 ：

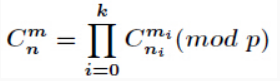
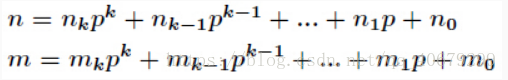
 这样将组合数的求解分解为小问题的乘积，下面考虑计算C(ni, mi) %p.

        已知C(n, m) mod p = n!/(m!(n - m)!) mod p。当我们要求（a/b）mod p的值，且b很大，无法直接求得a/b的值时，我们可以转而使用乘法逆元k，将a乘上k再模p，即(a*k) mod p。 其结果与(a/b) mod p等价。 　　 　　

        下面附上Lucas定理的一种证明，见下图，参考冯志刚《初等数论》第37页。 

代码实现上，可以分为递归版和非递归版。

由卢卡斯定理易知，$C(n, m) \%   p =  C(n / p, m / p) * C(n \% p, m \% p)   \% p$，如果$ C(n / p, m / p)$还是很大，就继续递归下去。

非递归版的相当于递归转化成循环迭代。其中求逆可以用费马小定理或扩展gcd。

//a^n % m
LL pow_mod(LL a, LL n, LL m)
{
    if (n == 0)  return 1;
    LL ans = pow_mod(a, n / 2, m);
    ans = ans * ans % m;
    if (n % 2)  ans = ans * a % m;
    return ans;
}

LL comp(LL a, LL b, LL m)
{
    if (a < b)  return 0;
    if (a == b)  return 1;
    if (b > a - b)  b = a - b;
    LL ans = 1, ca = 1, cb = 1;
    for (int i = 0; i < b; i++)
    {
        ca = ca * (a - i) % m;
        cb = cb * (b - i) % m;
    }
    ans = ca * pow_mod(cb, m - 2, m) % m;    //用的费马小定理
    return ans;
}

LL lucas(LL a, LL b, LL m)
{
    LL ans = 1;
    while (a && b)     //与
    {
        ans = (ans * comp(a % m, b % m, m)) % m;
        a /= m; b /= m;
    }
    return ans;
}

LL lucas2(LL a, LL b, LL p)
{
    return b ? lucas2(a / p, b / p, p) * comp(a % p, b % p, p) % p : 1;
}

参考链接：

1、https://blog.csdn.net/qq_40679299/article/details/80489761

 2、https://www.cnblogs.com/linyujun/p/5199684.html