计算机组成与设计（七）—— 除法器

除法的运算过程

与乘法相比，除法的实现较为复杂，运算过程如下：

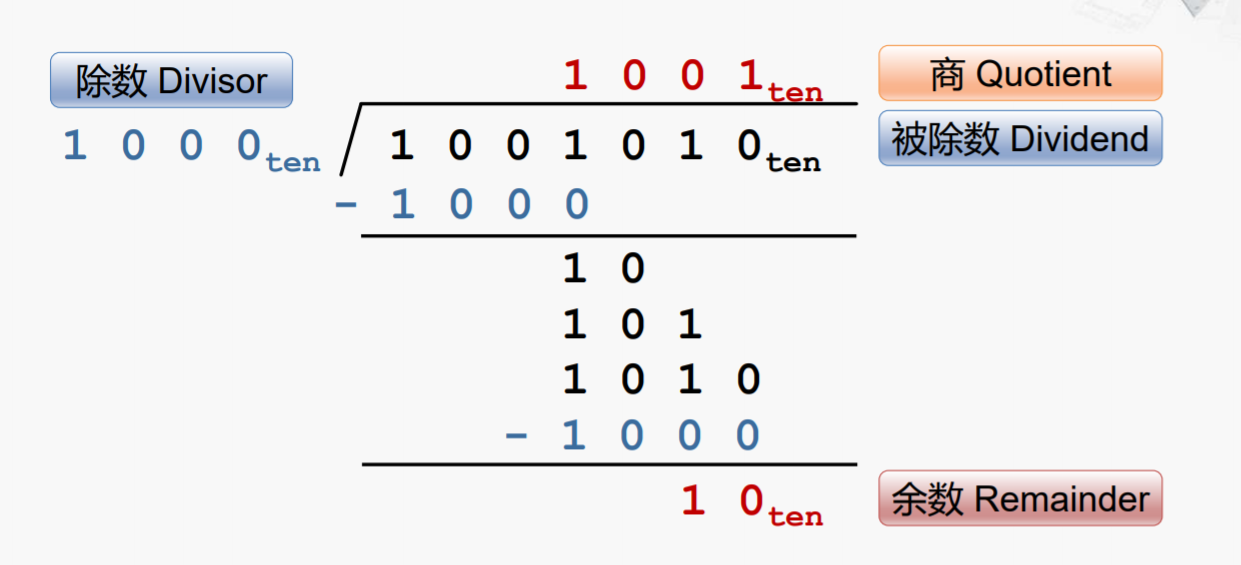
过程：

• 被除数和余数：将余数和被除数视为一个，共享一个寄存器，初始值为被除数
• 除数：可视为不断右移，并和被除数相减
• 商：每个bit依次生成，可视为不断左移

除法器的工作流程

要注意的是，与手算相比，电路实现总是将余数减除数，所以如果出现差小于0，要执行回退操作。

怎么会退呢？其实没有真正回退地方法，由于前面执行的是减法，回退只需加回来就可以了。

除法器的电路实现

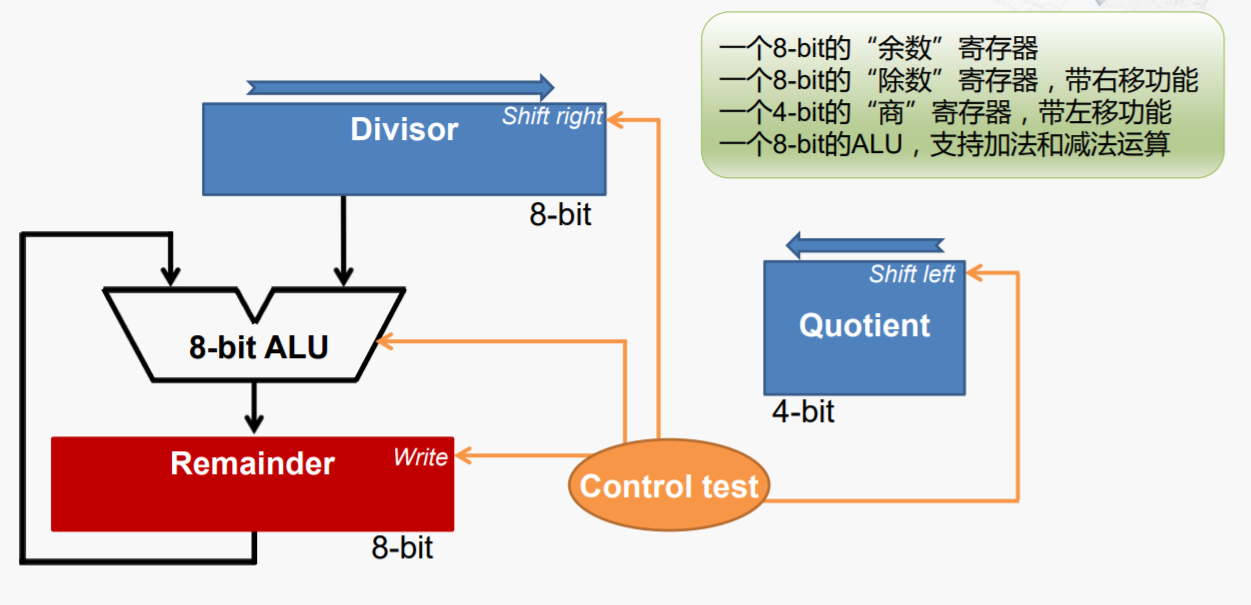
工作过程：

1. 初始化：将8-bit被除数放到“余数寄存器”，4-bit除数放到“除数寄存器”的高4位，将4-bit商寄存器置零
2. 执行减法运算：余数-除数，将结果放到“余数寄存器”
3. 检查余数寄存器的最高位（判断正负）。如果值小于0，回退，商左移，新的最右位设为0；如果值大于或等于0，商左移，新的最右位设为1.
4. 除数寄存器右移一位
5. 检查是否为最后一轮（本例为第5轮）

32-bit除法器同理可得

除法器的面积优化

对上面32-bit除法器从面积分析：

• “除数寄存器”实际只使用了一半
• “商寄存器”初始是空的，从左到右依次填满
• “余数寄存器”初始是满的，有实际意义的位每过一个周期从左到右依次减少

对应的，我们可以得到针对上述问题的方案：

• “除数寄存器”缩减为32-bit的，无需支持移位
• 取消“商寄存器”，商从右端逐位移入“余数寄存器”
• 64-bit ALU缩小为32-bit
• “余数寄存器”只有高32位参与加减法运算
• “余数寄存器”需要支持左移和右移
• 运算结束时，商占据“余数寄存器”的低32位

其中有两点需要注意：

1. 对优化的除法器右移，优化后的除法器的运算步骤是先相减再左移，比如0000,0111 / 0010, 每次做左移、减法，倒数第二步得到00110001,最后一次循环，减法再左移得到：00100011，因为真正的商是：0011， 而余数是0001。最终结果应该是先取低四位商，再右移取高四位余数。
2. 和乘法器一样，余数寄存器实际应该是65位而保证加法器的进位不会丢失。

参考链接：

1、https://www.coursera.org/learn/jisuanji-zucheng/discussions/weeks/5/threads/PdDS8dpvEeeC6xLrkeqqDg

2、https://www.coursera.org/learn/jisuanji-zucheng/lecture/z6vMq/407-chu-fa-qi-de-you-hua