前言:一个程序员前期可能需要各种业务和编程的能力,但是后期如果想要提高就需要有一个扎实的基础,厚积薄发,所以最近抽空学了下数据结构与算法,颇有感触,学习过程虽然很枯燥,但是坚持了下来,也收获了很多东西,准备总结一下自己得到的知识,一方面防止忘记,另一方面为更深入的知识面打打基础;接下来先介绍一下大概的知识框架
一、数据结构
对于需要输入大量数据,处理并且输出结果的算法,在输入输出数据或者处理数据的过程中,需要高效的存储和处理各种各样大量的数据。
在某些情况下,正是因为采用了高效的数据存储和管理方式,才使得某些巧妙地算法实现成为可能,而这种大量数据的存储,也就是数据结构了;
百度百科: 数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。记为: Data_Structure=(D,R) 其中D是数据元素的集合,R是该集合中所有元素之间的关系的有限集合。
数据结构具体指同一类数据元素中,各元素之间的相互关系,包括三个组成部分,数据的逻辑结构,数据的存储结构和数据运算结构。接下来的日子里我们研究的基本就是这些东西;
1 数据的逻辑结构
指反映数据元素之间的逻辑关系的数据结构,其中的逻辑关系是指数据元素之间的前后件关系,而与他们在计算机中的存储位置无关。
逻辑结构包括:
①、集合:数据结构中的元素除了同属一个集合之外,他们之间没有其他的关系;

②、线性:由0个或多个元素组成的有限数列,元素之间的关系为一对一;
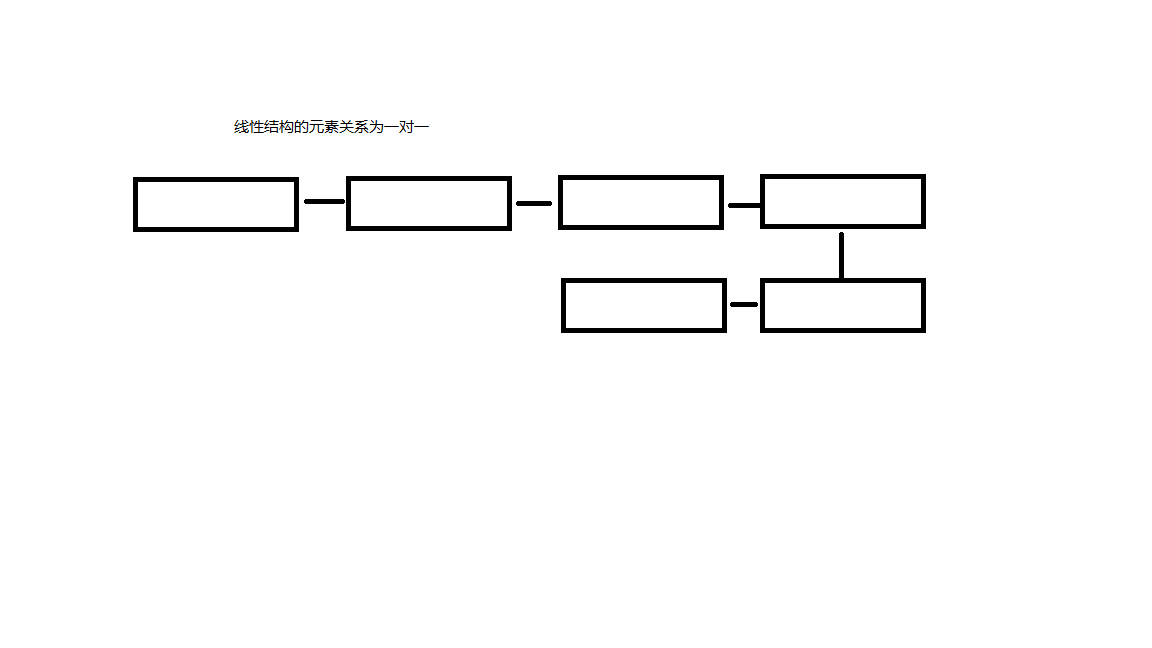
③、树:元素之间的关系为一对多,有且仅有一个特定的称为根(root)节点,是n个节点的有限级,当n为0时,称为空树;
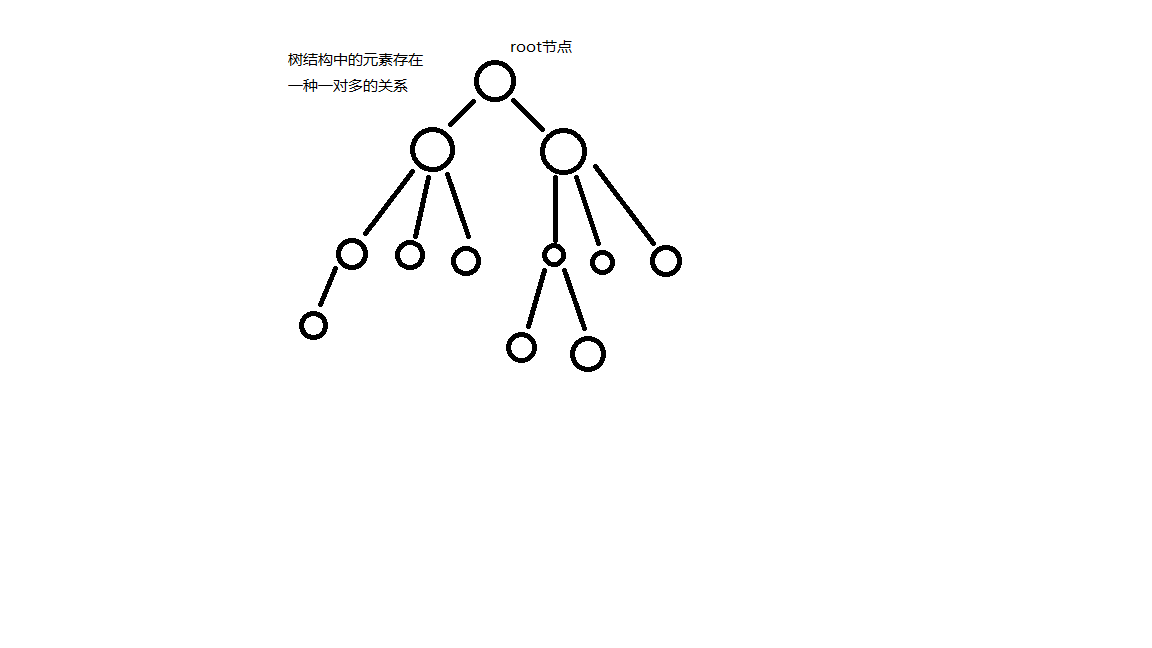

④、图:由顶点的有穷非空集合组成,通常表示为G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图中边的集合。元素之间的关系为多对多;


2 数据的存储结构
指数据的逻辑结构在计算机存储空间的存放形式。数据的物理结构是数据结构在计算机中的表示(又称映像)。由于具体实现的方法有顺序,链式,散列表等形式,所以一种数据逻辑结构可表示成一种或多种存储结构;
1、顺序存储:指把数据元素放在存储地址连续的存储单元;
优点:有序,增加和查询的时间复杂度O(1);
缺点:正因为有序所以在插入和删除时需要整体后移或前移,故时间复杂度为O(n);无法确定线性结构存储数据的长度;
2、链式存储:指把数据元素任意的放在地址的任意存储单元上,这组存储单元为可连续,也可为不连续;
优点:无序,插入和删除时操作物理空间简便,值需更换引用或指针,时间负责度为O(1);
缺点:增加和查询时需要的遍历,所以时间复杂度为O(n);
二、算法
1、什么是算法?
为了让计算机做出各种各样的处理,我们需要编写程序。为了让编写的程序“更加可靠、更加高效”,我们必须了解大量的算法,那么算法是什么?
听到算法这个词,大部分人都觉得好像很晦涩。的确,这不是一个常常能听到的词。事实上,在数学、计算机等理工科领域,所谓的算法,指的就是“对待问题的解决步骤”。而这里说的特定问题,通常有:
- 对信息进行排序
- 搜索目标信息
等不同的问题。
此外,如果说“算法是解决问题的步骤”,那么撇开计算机的数据处理不论,现实生活中也有很多问题的解决方法蕴含了算法的思想,比如菜谱。
而编写一段计算机程序一般都是实现一种已有的方法来解决某个问题。这种方法大多和使用的编程语言无关——它适用于各种计算机以及编程语言。是这种方法而非计算机程序本身描述了解决问题的步骤。在计算机科学领域,我们用算法这个词来描述一种有限、确定、有效的并适合用计算机程序来实现的解决问题的方法。
2、为什么学算法?
工作中经常会遇到各种问题,而这些问题大多都可以使用算法来解决并提升程序性能和存储,比如求1+2+…+9999+10000的和? 一般程序员:
int i, sum = 0, n = 10000; for(i=1; i <= n; i++){ sum = sum + i; } System.out.print(sum);
学过算法的程序员:
int i, sum = 0, n = 10000; sum = (1+n)*n/2; System.out.print(sum);
可能以计算机的神速,两个算法都可以秒杀解决掉!但是,如果我们把条件换成1加到1千万,或者1加到1千亿,差距就可想而知了,甚至人脑都可以比电脑计算得快了,所以对于走技术这条路上的程序猿来说,学算法还是非常有必要的。
3、算法的特性
输入:算法具有零个或多个输入;
输出:算法至少有一个或多个输出;
有穷性:指算法在执行有限的步骤之后,自动结束而不会出现无限循环,并且每一个步骤在可接受的时间内完成;
确定性:算法的每一个步骤都具有确定的含义,不会出现二义性;
可行性:算法的每一步都必须是可行的,也就是说,每一步都能够通过执行有限次数完成;
4、算法衍生的概念
时间复杂度
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度,记作:T(n)= O(f(n))。它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
这样用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法
第一种算法: int i, sum = 0, n = 100; // 执行1次 for( i=1; i <= n; i++ ) // 执行了n+1次 { sum = sum + i; // 执行n次 } 第二种算法: int sum = 0, n = 100; // 执行1次 sum = (1+n)*n/2; // 执行1次
第一种算法的时间复杂度为O(n),第二种算法的时间复杂度为O(1); 
常见的时间复杂度
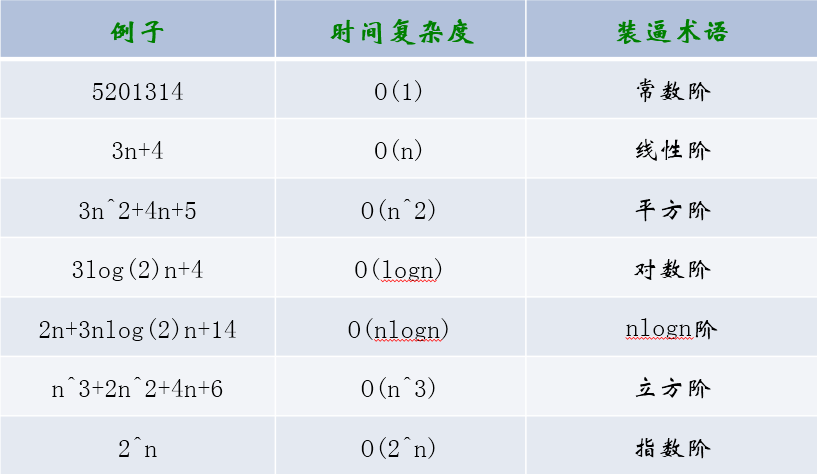
空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法的空间复杂度的计算公式记作:S(n)=O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
通常,我们都是用“时间复杂度”来指运行时间的需求,是用“空间复杂度”指空间需求。当直接要让我们求“复杂度”时,通常指的是时间复杂度。
显然对时间复杂度的追求更是属于算法的潮流! 通常,我们在写代码时,完全可以用空间换时间,提高性能。
三、常用的数据结构
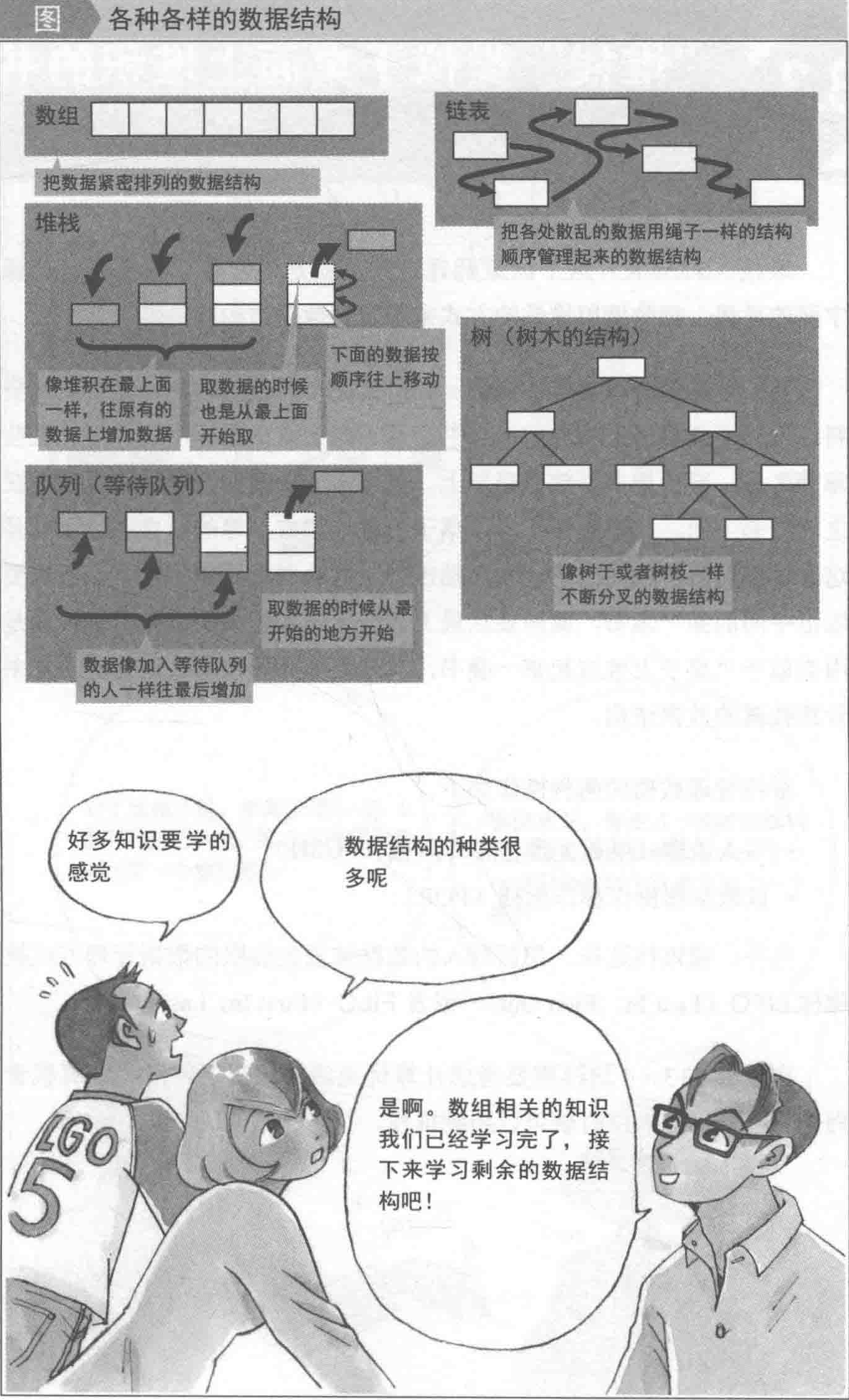
本系列参考书籍:
《写给大家看的算法书》
《图灵程序设计丛书 算法 第4版》