枚举固然可以,但是我还是想看看分层图。。。。
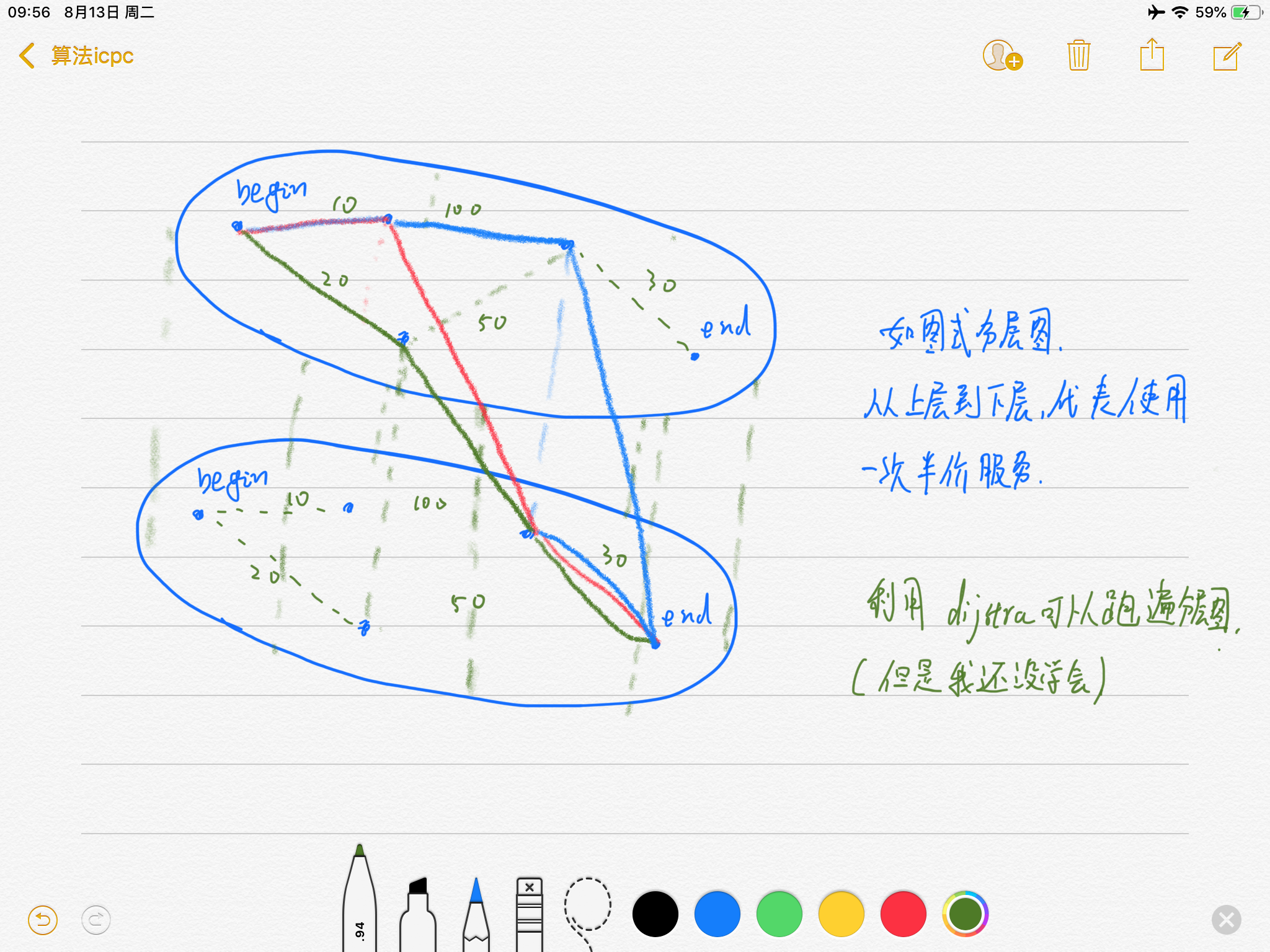
如本题所述 ,从上图到下图就是一个折扣的过程,上部分只有一种办法下去,下部分图没有办法去上面,该模型十分的巧妙啊!!!
下面我来演示一下自己改的样例吧
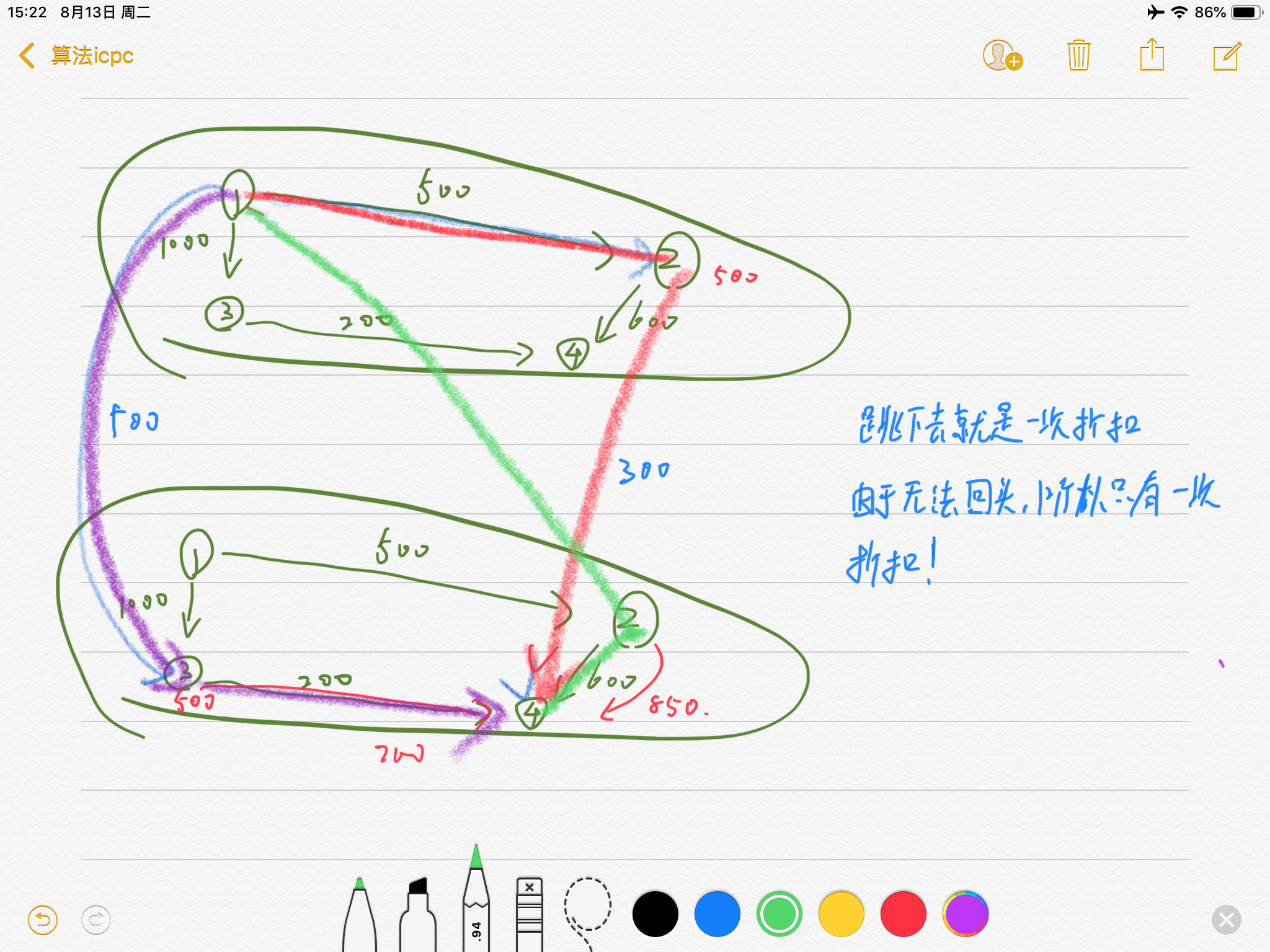
紫色路线是最短的,从上往下的路就是打折的路,类似bfs搜索,上面的所有点都可以下来,但是dijkstra只会只会保留最优的解
#include<cstring>
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<map>
#include<string>
using namespace std;
#define maxn 500000+10
typedef long long ll;
const long long INF = 2e14;
struct Node {
int p, tmp;
ll val;
Node(int a, ll b,int t) :p(a), val(b),tmp(t) {}
};
int n, m;
vector<Node>G[maxn];
bool operator < (const Node a, const Node b) {
if (a.val > b.val) return true;
else return false;
}
int vis[maxn][2];
ll dis[maxn][2];
void insert(int be, int en, ll len) {
G[be].push_back(Node(en, len, 0));
G[be].push_back(Node(en, len, 1));
return;
}
int dijkstra(int be) {
priority_queue<Node>que;
for (int i = 0; i <= n; i++) {
for (int j = 0; j < 2; j++) {
vis[i][j] = 0;
dis[i][j] = INF;
}
}
dis[be][0] = 0;
dis[be][1] = 0;
que.push(Node(be, 0, 0));
while (!que.empty()) {
Node ans = que.top();
que.pop();
if (vis[ans.p][ans.tmp] == 0) {
vis[ans.p][ans.tmp] = 1;
for (int i = 0; i < G[ans.p].size(); i++) {
int p = G[ans.p][i].p;
int t = G[ans.p][i].tmp;//确定位置
if (!vis[p][t] && dis[p][t] > dis[ans.p][t] + G[ans.p][i].val) {
dis[p][t] = G[ans.p][i].val + dis[ans.p][t];
que.push(Node(p, dis[p][t], t));
}
if (t == 0) {//可以下来的话
if (!vis[p][1] && dis[p][1] > dis[ans.p][0] + G[ans.p][i].val / 2) {//从上面穿下来所以是0加给1
dis[p][1] = dis[ans.p][0] + G[ans.p][i].val/2;
que.push(Node(p, dis[p][1], 1));
}
}
}
}
}
return 0;
}
map<string, int>ins;
int main() {
while (~scanf("%d %d", &n, &m)) {
ins.clear();
for (int i = 0; i <= n; i++)G[i].clear();
string be, en;
ll len;
int cnt = 1;
while (m--) {
cin >> be >> en;
scanf("%lld", &len);
if (ins[be] == 0) ins[be] = cnt++;
if (ins[en] == 0) ins[en] = cnt++;
insert(ins[be], ins[en], len);
}
cin >> be >> en;
if (ins[be] == 0) ins[be] = cnt++;
if (ins[en] == 0) ins[en] = cnt++;
dijkstra(ins[be]);
if (dis[ins[en]][1] == INF) printf("-1
");
else printf("%lld
", dis[ins[en]][1]);
}
return 0;
}