1、张量
几何代数中定义的张量是基于向量和矩阵的推广,通俗一点理解的话,我们可以将标量视为零阶张量,矢量视为一阶张量,那么矩阵就是二阶张量。
例如,可以将任意一张彩色图片表示成一个三阶张量,三个维度分别是图片的高度、宽度和色彩数据。将这张图用张量表示出来,就是最下方的那张表格:
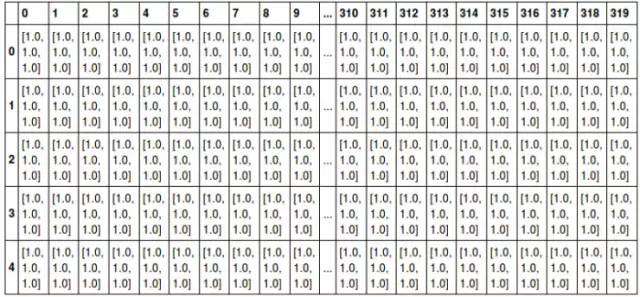
其中表的横轴表示图片的宽度值,这里只截取0~319;表的纵轴表示图片的高度值,这里只截取0~4;表格中每个方格代表一个像素点,比如第一行第一列的表格数据为[1.0,1.0,1.0],代表的就是RGB三原色在图片的这个位置的取值情况(即R=1.0,G=1.0,B=1.0)。
当然我们还可以将这一定义继续扩展,即:我们可以用四阶张量表示一个包含多张图片的数据集,这四个维度分别是:图片在数据集中的编号,图片高度、宽度,以及色彩数据。
张量在深度学习中是一个很重要的概念,因为它是一个深度学习框架中的一个核心组件,后续的所有运算和优化算法几乎都是基于张量进行的。
2、范数
有时我们需要衡量一个向量的大小。在机器学习中,我们经常使用被称为范数(norm) 的函数衡量矩阵大小。Lp 范数如下:
所以:
L1范数:为x向量各个元素绝对值之和;
L2范数:为x向量各个元素平方和的开方。
这里先说明一下,在机器学习中,L1范数和L2范数很常见,主要用在损失函数中起到一个限制模型参数复杂度的作用,至于为什么要限制模型的复杂度,这又涉及到机器学习中常见的过拟合问题。具体的概念在后续文章中会有详细的说明和推导,大家先记住:这个东西很重要,实际中经常会涉及到