前段时间,有朋友发了我一份算法题,说是国际软件大赛的训练题,本人闲来做了一道看起来很有意思的题,费话不多说,先来看原题:
Exercise 25 : Rescuing Robin (programminga simple game)
Seen fromthe sky, the skyscrapers of Gotham City form a 10x10 checkerboardand the gap between two skyscrapers is one. The joker has harmed Robin and lefthim on the roof of a randomly chosen skyscraper in Gotham City.
To saveRobin, Batman, who is randomly parachuted on another roof, has to jump fromroof to roof until he reaches Robin but he just has time enough for 25 jumps.Fortunately, he has a sensor that gives him his distance to Robin but thedistance is expressed as the sum of the X and Y gaps between Batman’s andRobin’s positions.
At eachstage, Batman is informed by his bat-computer of his x-y position, of thenumber of jumps he has left and of his distance to Robin. He then chooses theamplitude of his displacement in X and Z. If he lands outside the roofscheckerboard, he dies; if he has globally jumped more than 25 times withoutreaching Robin, he dies of embarrassment. In all other cases, the gamecontinues until he finds Robin. 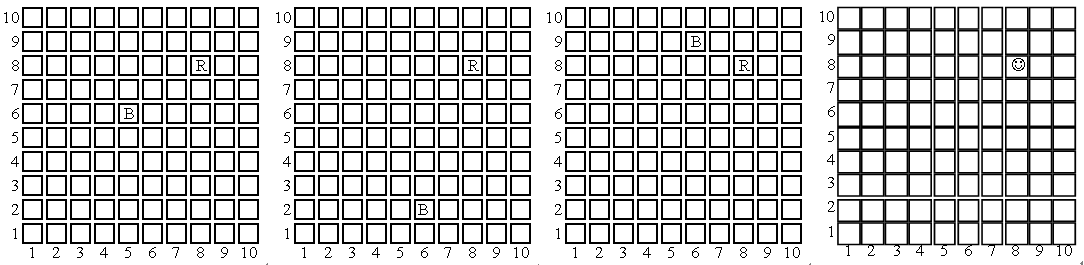
Game example:
|
Position : 5,6 Jumps left : 25 Dist. to Robin : 5 Move? 1,-4 |
Position : 6,2 Jumps left: 20 Dist. to Robin : 8 Move? 0,7 |
Position : 6,9 Jumps left: 13 Dist. to Robin : 3 Move? 2,1 |
Batman saves Robin! Jumps used : 15 |
Write analgorithm that implements this game.
粗略看了一下,题目基本前面说了一堆费话,关键的其实就是说罗宾(以下简称R)被抓走了,蝙蝠侠(以下简称B)要去救他,而他们两个目前的位置都是随机出现在10X10的楼顶上,且不在同一个楼顶,B不知道R的方向,却有一个追踪器可以知道当前距R的距离。现在B可以在两个相邻的楼顶间最多跳跃25次,以找到R(解救),则游戏成功;如果B跳了25次仍未找到R(自杀),则游戏失败;如果B跳出了楼层(摔死),则游戏也失败。
先来定义几个必需要用变量:
出发坐标 B(x1,y1) 目的坐标 R(x2,y2) 两者当前的距离 Dcur
我的理解就是一个搜索问题,启发函数便是两者的距离,但是由于这个函数并不能进行像传统的方法一样,可以进行子节点预算(追踪器只能得到当前点距目标的距离),所以还需要进行一些辅助手段。
我这里首先想到的是深度优先搜索,但是由于并不能预测子节点的启发函数,所以不能直接套用,需要对其进行改进。
另外,我还想到了利用数学方程,本来以为是个二元方程组,但是后来仔细考察了原文“Batman, who is randomly parachuted on another roof”,他是随机伞投下来的,而且题中并没有说有设备或者人能告诉他所处的位置,所以笔者认为B对自己所处的坐标也是不知道的,于是这是一个四元(B与R的坐标)带绝对值的方程组:
Dcur = |x1-x2| + |y1 - y2|,其中x1,x2,y1,y2∈[1,10]
本人数学真心不好,加上这个方程组要想解出来,最少要有四个方程,也就是说最少B要无为地跳跃四次,然后自己再在楼顶解了这个四元一次带绝对值的条件限定方程组,个人感觉非常的不合理,虽然说这从理论上可能是解决问题浪费跳跃步数很少的方法。
还是回到深度优先搜索上来,审题,发现可以利用到的地方(常理)是,B可以看到自己所在楼层的四周是否还有楼层,即自己是否正处在楼层边缘。于是笔者考虑可以使用带方向选择的深度优先搜索算法,基本思路是:B跳跃时优先横向,以找到R所在的列,然后再竖向跳,以找到R。具体如下:
定义跳跃方向标记,初始都为“停”:
ppe:停、前、后 上上次跳跃方向
pre :停、前、后 上一次跳跃方向
cur :停、前、后 当前跳跃方向
距离标记:
距离Dpre 上一次所处楼顶与目标的距离
距离Dcur 当前所处楼顶与目标的距离
跳跃数:step
这里有三个方向标记,主要作用就是识别B是否已经找到了R所在的行或者列,而距离标记则是用来比较是否跳错了方向,寻找R的原理如下图所示:

假设B和R处在如图所示的位置,B首先往右横向跳跃,发现距离增大了,于是返回,一直跳,直到距离再次又增大了(也有可能B到了左边缘),返回一步,于是这就是R所在的列。如图,经过7步后,通过验证条件(ppe==pre且cur与之相反),来确定R的所在列。
当R的列确定后,我们所要做的就变成了竖向跳跃,方法与横向类似,却更为简单,并不需要pre和ppe标记了,而只用找到正确的方向,一直跳就能找到R了。
下面是我正式提出的算法:
1、生成两个不同的位置B(x1,y1),R(x2,y2),cur=|x2-x1|+|y2-y1|,step=0,方向标记设置为停;
2、将B的初始位置入栈,计算距离cur;
3、横向移动(随机但不跳楼),设置横向cur=当前移动方向,step+1;
重复{
Dpre=Dcur,计算距离Dcur;
如果找到Robin,则成功结束;
如果step=25,则失败结束;
如果 距离Dcur>距离Dpre :
出栈,往出栈后的点移动,令ppe=pre,pre=cur,再将cur反向;
否则:
将当前点进栈;
如果 ppe==pre且ppe与cur相反 或者 已经在左右边缘了 (此处就是Robin的所在列):
cur=停,跳出循环;
否则:
继续延着cur的方向跳,令ppe=pre,pre=cur;
step+1;
}
此时,已经确定了Robin的所在列了,接下来就是行,方法类似,只是更加简单:
4、竖向移动(随机但不跳楼),设置竖向cur=当前移动方向,step+1;
重复{
Dpre=Dcur,计算距离Dcur;
如果找到Robin,则结束;
如果step=25,游戏结束;
如果 距离Dcur>距离Dpre :
出栈,往出栈后的点移动,将cur反向;
否则:
将当前点进栈;
继续延着cur的方向跳;
step+1;
}
4、输出结果,栈里面存的是最佳路径,寻找的实际路径只需要另外用一个列表在每次跳跃时记录下来就行
那么这个算法的效率如何呢,显然,它的时间复杂度是n,空间复杂度为1。当B降落在四个角时,最大浪费步数为2步;当B降落在边缘时,最大浪费频数为4步;当B降落在中间时,最大浪费步数为6步;而题中所给的最大步数为25,楼层是10X10,所以无论B与R初始化坐标为什么,B都能成功到达R的位置。
转载请注明原址:http://www.cnblogs.com/lekko/archive/2012/07/19/BatmanSaveRobin.html
本人小菜一名,刚开博客,文笔浅略,望各位见谅,下面附上实现代码:
 View Code
View Code
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <time.h> 4 /** 算法说明 5 ** 当Batman降落在角落时,最大浪费步数为2步 6 ** 当Batman降落在边缘时,最大浪费步数为4步 7 ** 当Batman降落在中间时,最大浪费步数为6步 8 **/ 9 10 // 一些参数 11 #define True 1 // 定义真 12 #define False 0 // 定义假 13 #define gSize 10 // 方格大小 14 #define gMaxStep 25 // 最大步数 15 16 // 所在位置 17 typedef struct{ 18 int x; 19 int y; 20 }Position; 21 // 位置标记 22 enum Indicating{ 23 stop=0, 24 backward, // 左,下 25 forward // 右,上 26 }; 27 28 // 函数声明 29 int GetDistance(); 30 enum Indicating GetIndicate(int); 31 void Jump(Indicating,bool); 32 void PrintPath(); 33 34 // 全局变量 35 int step,index; // 跳跃步数,最佳路径的索引 36 Position Pb,Pr; // Batman、Robin的坐标 37 Position bestPath[25]; // 行动的最佳路径 38 Position realPath[25]; // 行动的真实路径 39 40 void main() 41 { 42 int preDst,curDst; // 距离 43 enum Indicating ppe,pre,cur; // 方向标示 44 45 // 生成随机位置 46 srand((unsigned)time(NULL)); // 初始化随机函数 47 do 48 { 49 Pb.x = rand()%gSize+1; 50 Pb.y = rand()%gSize+1; 51 Pr.x = rand()%gSize+1; 52 Pr.y = rand()%gSize+1; 53 } while (Pr.x==Pb.x && Pr.y==Pb.y); // 两个点要不相同 54 55 // 初始化 56 curDst = GetDistance(); // 计算初始距离 57 step = 0; // 步数为0 58 index = 0; // 索引为0 59 ppe = pre = cur = stop; // 方向为停 60 bestPath[index++] = Pb; // 记录初始位置 61 realPath[step] = Pb; 62 63 // 第一次跳 64 cur = GetIndicate(Pb.x); // 决定跳的方向 65 Jump(cur,True); // 横向跳 66 /***** 横向移动 *****/ 67 while(++step<=gMaxStep) // 不超过最大步数 68 { 69 preDst = curDst; 70 curDst = GetDistance(); 71 if (!curDst) break; // 找到了Robin 72 if (step==gMaxStep) break; // 步数到了上限,不用继续了 73 if (curDst>preDst) // 距离变大,方向错了 74 { 75 ppe = pre; // 上上步方向 76 pre = cur; // 上一步方向 77 cur = ((cur==backward)?forward:backward); // 当前方向反向 78 Jump(cur,True); // 返回上一步 79 --index; // 最佳路径的索引不变(原先是+1了的) 80 } 81 else // 距离缩小,方向没错 82 { 83 bestPath[index++] = Pb; 84 // 如果找到了Robin所在列 85 if ((ppe==pre && ((ppe==backward&&cur==forward)||(ppe==forward&&cur==backward)))|| Pb.x==1 || Pb.x==gSize) 86 break; // 跳出循环 87 else // 否则 88 { 89 ppe = pre;pre = cur; 90 Jump(cur,True); // 继续沿着当前的方向跳 91 } 92 } 93 } 94 // 没找到了Robin且步数还够 95 if ((curDst && step<gMaxStep)) 96 { 97 /***** 竖向移动 *****/ 98 cur = GetIndicate(Pb.y); // 竖向移动的方向 99 Jump(cur,False); // 竖向跳 100 while(++step<=gMaxStep) 101 { 102 preDst = curDst; 103 curDst = GetDistance(); 104 if (!curDst) break; // 找到了Robin 105 if (step==gMaxStep) break; 106 if (curDst>preDst) // 反向 107 { 108 cur = ((cur==backward)?forward:backward);--index; 109 } 110 else 111 bestPath[index++] = Pb; 112 Jump(cur,False); // 跳 113 } 114 } 115 // 找到了Robin 116 if (!curDst) 117 { 118 bestPath[index] = Pb; // 最佳路径的最后一个点 119 printf("The Batman has used %i step%c to find Robin!\n",step,(step==1?' ':'s')); 120 } 121 else 122 printf("The Batman didn't found Robin,he has dead!\n"); 123 PrintPath(); // 打印路径 124 getchar(); 125 } 126 // 获取两点距离 127 // 参数:点x,点y 128 int GetDistance() 129 { 130 return abs(Pb.x-Pr.x)+abs(Pb.y-Pr.y); 131 } 132 // 获取移动方向 133 // 参数:当前位置 134 enum Indicating GetIndicate(int x) 135 { 136 if (x==1) // 在左、上边缘 137 return forward; 138 else if (x==gSize) // 在右、下边缘 139 return backward; 140 return (enum Indicating)(rand()%2 +1); // 随机 141 } 142 // 根据当前方向跳 143 // 参数:当前方向,是否横向 144 void Jump(enum Indicating idc,int IsHorizonal) 145 { 146 if (IsHorizonal) 147 { 148 if (idc==forward) // 往右跳 149 ++Pb.x; 150 else // 往左跳 151 --Pb.x; 152 } 153 else 154 { 155 if (idc==forward) // 往上跳 156 ++Pb.y; 157 else // 往下跳 158 --Pb.y; 159 } 160 realPath[step+1] = Pb; // 记录真实路径 161 } 162 // 打印路径 163 void PrintPath() 164 { 165 int i; 166 printf("Batman was started in (%i,%i)\n",realPath[0].x,realPath[0].y); 167 printf("Robin was in (%i,%i)\n",Pr.x,Pr.y); 168 printf("The real way is:\n"); 169 for(i =0;i<=step;++i) 170 printf("(%i,%i) ",realPath[i].x,realPath[i].y); 171 printf("\nThe best way is:\n"); 172 for(i=0;i<=index;++i) 173 printf("(%i,%i) ",bestPath[i].x,bestPath[i].y); 174 }
