JZOJ 4313. 【NOIP2015模拟11.4】电话线铺设

题目

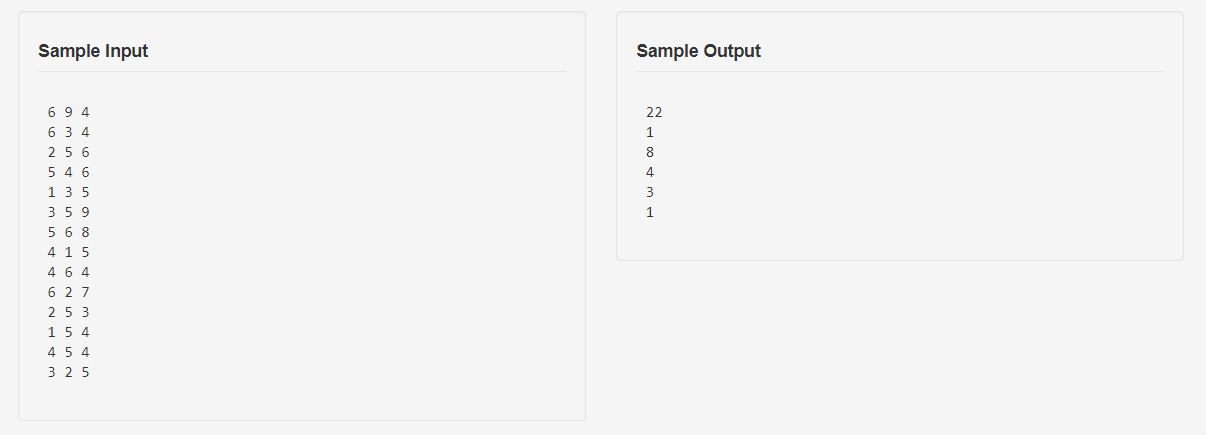
思路

先求只用王牌电缆的最小生成树
再选一条李牌电缆替换王牌电缆
使答案最小就完了
假如要替换的李牌电缆两端点是 (u,v)
那么生成树中 (u Longrightarrow lca(u,v)) 和 (v Longrightarrow lca(u,v)) 这两条链中的权值最大的边就是要替换的边
类似于次小生成树
倍增维护就好了

注意，有可能只用王牌电缆无法构成最小生成树
这里特判一下，此时跑最小生成树最终的结果必然是两个不连通的集合
这使枚举的李牌电缆就要使它们联通，求一个最小的李牌电缆即可

#include<cstdio>
#include<algorithm>
using namespace std;

const int N = 2e5 + 5;
int n , W , L , h[N] , fa[N] , tot , vis[N] , size[N] , lw , lid , hl;
int f[N][20] , anc[N][20] , ind[N][20] , dep[N] , ans , s , rt;

struct edge{
	int nxt , to , w , id;
}e[N << 1];

struct Edge{
	int u , v , w , id;
}E[N];

struct Edge1{
	int u , v , w;
}l[N];

inline void addedge(int u , int v , int w , int id)
{
	e[++tot] = (edge){h[u] , v , w , id};
	h[u] = tot;
}

inline bool cmpE(Edge x , Edge y){return x.w < y.w;}
inline int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}

inline bool merge(int x , int y)
{
	int xx = find(x) , yy = find(y);
	if (fa[xx] != fa[yy]) 
	{
		if (size[xx] < size[yy]) fa[xx] = fa[yy] , size[yy] += size[xx];
		else fa[yy] = fa[xx] , size[xx] += size[yy];
		return 1;
	}
	return 0;
}

inline void Kruskal()
{
	int u , v , w;
	for(register int i = 1; i <= W; i++)
		scanf("%d%d%d" , &E[i].u , &E[i].v , &E[i].w) , E[i].id = i;
	sort(E + 1 , E + W + 1 , cmpE);
	for(register int i = 1; i <= n; i++) fa[i] = i , size[i] = 1;
	for(register int i = 1; i <= W; i++)
	{
		if (merge(E[i].u , E[i].v))
		{
			ans += E[i].w , s++;
			vis[E[i].id] = 1;
			addedge(E[i].u , E[i].v , E[i].w , E[i].id);
			addedge(E[i].v , E[i].u , E[i].w , E[i].id);
			if (!rt) rt = E[i].u;
		}
		if (s == n - 1) break;
	}
}

inline void dfs(int x , int father)
{
	for(register int i = 1; i <= 17; i++)
	if (f[x][i - 1])
	{
		f[x][i] = f[f[x][i - 1]][i - 1];
		if (anc[x][i - 1] < anc[f[x][i - 1]][i - 1])
			anc[x][i] = anc[f[x][i - 1]][i - 1] , ind[x][i] = ind[f[x][i - 1]][i - 1];
		else anc[x][i] = anc[x][i - 1] , ind[x][i] = ind[x][i - 1];
	}
	else break;
	
	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == father) continue;
		f[v][0] = x , dep[v] = dep[x] + 1 , anc[v][0] = e[i].w , ind[v][0] = e[i].id;
		dfs(v , x);
	}
}

inline void update(int ll , int u , int v)
{
	if (dep[u] < dep[v]) swap(u , v);
	int deep = dep[u] - dep[v] , sum;
	int t = -0x3f3f3f3f , id;
	for(register int i = 0; i <= 17; i++)
	if (deep & (1 << i))
	{
		if (t < anc[u][i]) t = anc[u][i] , id = ind[u][i];
		u = f[u][i];
	}
	if (u == v)
	{
		sum = ans - t + l[ll].w;
		if (sum < lw) lw = sum , lid = ll , hl = id;
		return;
	}
	for(register int i = 17; i >= 0; i--)
	if (f[u][i] != f[v][i])
	{
		if (t < anc[u][i]) t = anc[u][i] , id = ind[u][i];
		if (t < anc[v][i]) t = anc[v][i] , id = ind[v][i];
		u = f[u][i] , v = f[v][i];
	}
	if (t < anc[u][0]) t = anc[u][0] , id = ind[u][0];
	if (t < anc[v][0]) t = anc[v][0] , id = ind[v][0];
	
	sum = ans - t + l[ll].w;
	if (sum < lw) lw = sum , lid = ll , hl = id;
}

inline void getans()
{
	for(register int i = 1; i <= L; i++) scanf("%d%d%d" , &l[i].u , &l[i].v , &l[i].w);
	if (s != n - 1)
	{
		int Min = 0x3f3f3f3f , ld = 0;
		for(register int i = 1; i <= L; i++)
		if (find(l[i].u) != find(l[i].v) && l[i].w < Min)
			Min = l[i].w , ld = i;
		printf("%d
" , ans + Min);
		for(register int i = 1; i <= W; i++)
		if (vis[i]) printf("%d
" , i);
		printf("%d
" , ld);
		return;
	}
	dfs(rt , 0);
	lw = 0x3f3f3f3f;
	for(register int i = 1; i <= L; i++) update(i , l[i].u , l[i].v);
	printf("%d
" , lw) , vis[hl] = 0;
	for(register int i = 1; i <= W; i++) 
	if (vis[i]) printf("%d
" , i);
	printf("%d
" , lid);
}

int main()
{
	freopen("telephone.in" , "r" , stdin);
	freopen("telephone.out" , "w" , stdout);
	scanf("%d%d%d" , &n , &W , &L);
	Kruskal();
	getans();
}