李超树
它本质上是线段树的拓展运用
解决的问题:平面直角坐标系中,支持插入线段,问 \(x = x_0\) 这条直线上最大的 \(y\) 值
它维护的东西很奇特:优势线段
何为“优势线段”?
给定两条线在指定区间内,所有 \(x\) 对应的两个 \(y\) 高的数量越多的就是优势线段
如下
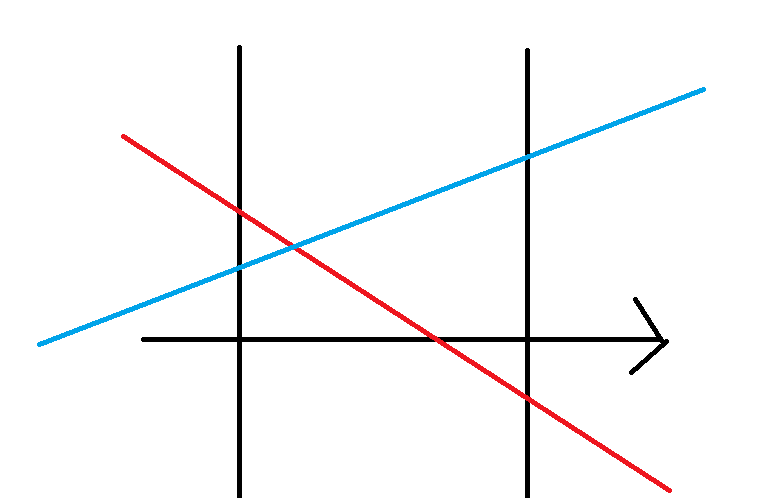
蓝线便是优势线段
我们在线段树对应的本区间就维护蓝线的斜率和截距就行了
不过红线不能就此抛弃,而应让它下放到它可能具有优势的区间
这样的话,我们需要把询问所在的区间跑完才能弄出答案
因为正确答案可能已经被下放到了比较靠下的地方,即更小的区间
以上是大致思路,具体过程如下
- 此刻区间里面还没有维护的东西,那么直接更新线段树信息即可
- 新线段与此刻线段树维护的线段没有交点,如果新线段在线段树维护的线段树之上,那么直接更新,否则 \(return\)
- 新线段与此刻线段树维护的线段有交点,那么就需要分类讨论了。
当交点的 \(x\) 轴坐标在区间正中心的左侧时,如果新线段的斜率高于原线段,那么很明显线段树维护的值就要变成新线段了(上面的图就是这种情况),但在变成新线段之前要把原线段的信息下放到左子树(即交点所在的半个原区间)。若斜率低于原线段,那么本区间的优势线段没有变,就直接递归讨论线段树的左儿子即可。右侧同理,具体见例题代码。
最好自己手划一下,然后打一遍标程,再对一遍标程就会板了
时间复杂度:插入直线时,每次将直线的定义域分隔到 \(\log n\) 个区间,每个区间最多把标记下传 \(\log n\) 层,因此修改的时间复杂度为 \(\log(n^2)\)。(但常数不大)
总的复杂度是:\(nlog(n^2)\)
例题:
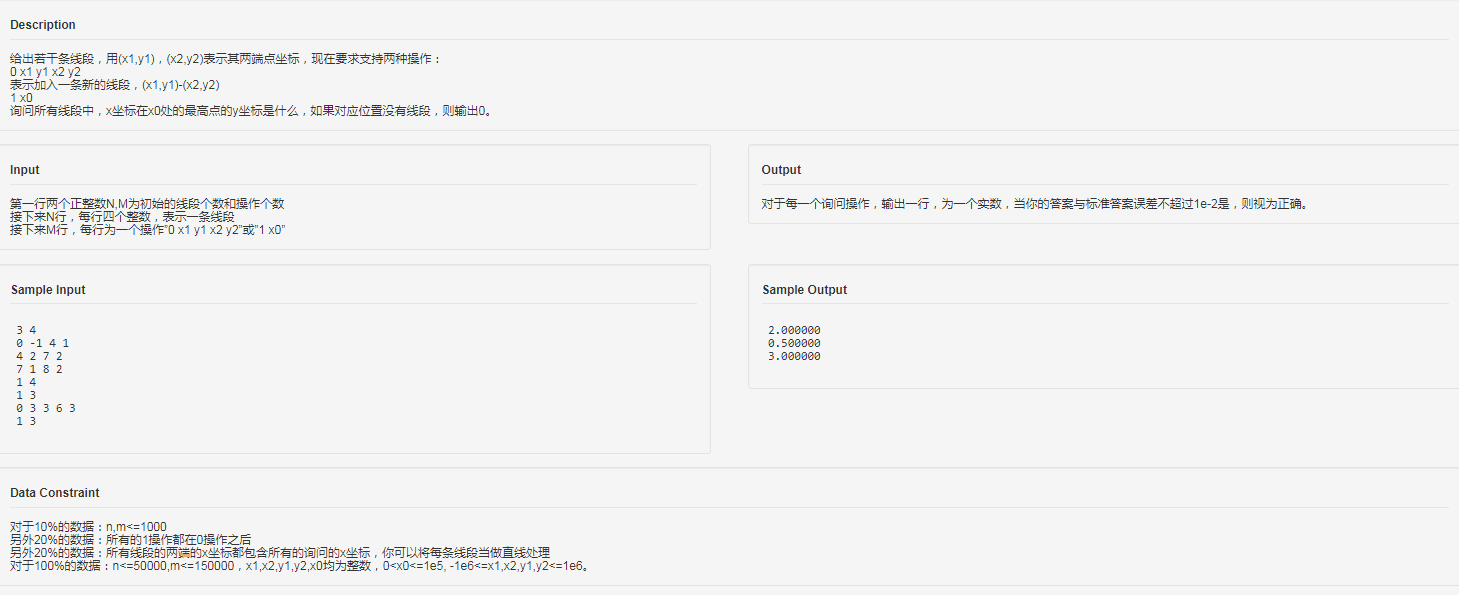
思路分析:裸题,直接上李超树
注意:加的是线段!即区间加入一条线段而非直线
而题中只需维护 \([1..10^5]\) 中线段的信息就行了
板子
\(Code\)
#include<cstdio>
using namespace std;
const int N = 1e5 + 5;
int n , m , fl[4 * N];
struct tree{
long double k , b;
}seg[4 * N];
inline void swap(int &x , int &y){int t = x; x = y , y = t;}
inline long double max(long double x , long double y){return x < y ? y : x;}
inline long double min(long double x , long double y){return x < y ? x : y;}
inline long double Intersection(long double k1 , long double b1 , long double k2 , long double b2){return 1.0 * (b2 - b1) / (k1 - k2);}
inline void update(long double k , long double b , int x , int y , int l , int r , int rt)
{
if (y < l || x > r) return;
int mid = (l + r) >> 1;
if (l >= x && r <= y)
{
if (!fl[rt])
{
seg[rt].b = b , seg[rt].k = k , fl[rt] = 1;
return;
}
long double f1 = seg[rt].k * l + seg[rt].b , f2 = seg[rt].k * r + seg[rt].b;
long double f3 = k * l + b , f4 = k * r + b;
if (f1 >= f3 && f2 >= f4) return;
else if (f1 <= f3 && f2 <= f4) seg[rt].k = k , seg[rt].b = b;
else{
long double len = Intersection(k , b , seg[rt].k , seg[rt].b);
if (f1 <= f3)
{
if (len <= mid) update(k , b , x , y , l , mid , rt << 1);
else update(seg[rt].k , seg[rt].b , x , y , mid + 1 , r , rt << 1 | 1) , seg[rt].k = k , seg[rt].b = b;
}
else{
if (len > mid) update(k , b , x , y , mid + 1 , r , rt << 1 | 1);
else update(seg[rt].k , seg[rt].b , x , y , l , mid , rt << 1) , seg[rt].k = k , seg[rt].b = b;
}
}
return;
}
if (x <= mid) update(k , b , x , y , l , mid , rt << 1);
if (y > mid) update(k , b , x , y , mid + 1 , r , rt << 1 | 1);
}
inline long double query(int l , int r , int rt , int x)
{
long double ans = 1.0 * x * seg[rt].k + seg[rt].b;
if (l == r) return ans;
int mid = (l + r) >> 1;
if (x <= mid) ans = max(ans , query(l , mid , rt << 1 , x));
else ans = max(ans , query(mid + 1 , r , rt << 1 | 1 , x));
return ans;
}
int main()
{
freopen("query.in" , "r" , stdin);
freopen("query.out" , "w" , stdout);
scanf("%d%d" , &n , &m);
int x1 , x2 , y1 , y2;
long double k , b;
for(register int i = 1; i <= 4 * 1e5 + 1; i++) seg[i].b = -1e18 , seg[i].k = 0;
for(register int i = 1; i <= n; i++)
{
scanf("%d%d%d%d" , &x1 , &y1 , &x2 , &y2);
if (x1 > x2) swap(x1 , x2) , swap(y1 , y2);
if (x1 == x2) k = 0 , b = max(1.0 * y1 , 1.0 * y2);
else k = 1.0 * (y1 - y2) / (x1 - x2) , b = 1.0 * y1 - 1.0 * k * x1;
update(k , b , x1 , x2 , 1 , 1e5 , 1);
}
int opt;
while(m--)
{
scanf("%d" , &opt);
if (opt == 0)
{
scanf("%d%d%d%d" , &x1 , &y1 , &x2 , &y2);
if (x1 > x2) swap(x1 , x2) , swap(y1 , y2);
if (x1 == x2) k = 0 , b = max(1.0 * y1 , 1.0 * y2);
else k = 1.0 * (y1 - y2) / (x1 - x2) , b = 1.0 * y1 - 1.0 * k * x1;
update(k , b , x1 , x2 , 1 , 1e5 , 1);
}
else{
scanf("%d" , &opt);
long double ans = query(1 , 1e5 , 1 , opt);
printf("%.6Lf\n" , ans == -1e18 ? ans = 0 : ans);
}
}
}