1. GC标记-清除算法(Mark Sweep GC)

• 世界上第一个GC算法，由 JohnMcCarthy 在1960年发布。

---

标记-清除算法由标记阶段和清除阶段构成。

1. 标记阶段就是把所有的活动对象都做上标记的阶段。

   • 标记阶段就是“遍历对象并标记”的处理过程。
   • 标记阶段经常用到深度优先搜索。

   mark_pahase(){
       for(r : $roots)
           mark(*r)
   }
   
   mark(obj){
       if(obj.mark == FALSE)
           obj.mark = TRUE
           for(child : children(obj))
               mark(*child)
   }
   

2. 清除阶段就是把那些没有标记的对象，也就是非活动对象回收的阶段。

   • 清除阶段collector会遍历整个堆，回收没有打上标记的对象（即垃圾）。
   • 内存的合并操作也是在清除阶段进行的。

   sweep_phase(){
       sweeping = $heap_start
       while(sweeping < $heap_end)
           if(sweeping.mark == TRUE)
               sweeping.mark = FALSE
           else
               sweeping.next = $free_list
               $free_list = sweeping
           sweeping += sweeping.size
   }
   

---

1. 分配

• 分配指将回收的内存空间进行再利用。

  -> 伪代码描述内存分配
  
  new_obj(size){
      chunk = pickup_chunk(size, $free_list)
      if(chunk != NULL)
          return chunk
      else
          allocation_fail() # 大招，销毁并释放全部空间
  }
  

2. 合并

• 合并指将连续的小分块连在一起形成一个大分块

  -> 伪代码描述合并操作
  
  sweep_phase() {
      sweeping = $heap_start
      while(sweeping < $heap_end)
          if(sweeping.mark == TRUE)
              sweeping.mark = FALSE
          else
              if(sweeping == $free_list + $free_list.size)
                  $free_list.size += sweeping.size
              else
                  sweeping.next = $free_list
                  $free_list = sweeping
          sweeping += sweeping.size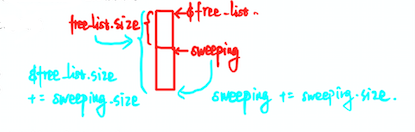
  }
  

  

---

优点

1. 实现简单
2. 与保守式GC算法兼容

缺点

1. 碎片化(fragmentation)

   • 使用过程中会逐渐产生被细化的分块

2. 分配速度

   • 分块不连续，每次分配都必须遍历空闲链表，以便找到足够大的分块。
   • 最糟的情况就是每次分配都要遍历全部空闲链表

3. 与写时复制技术(copy-on-write)不兼容

   • 写时复制技术在重写时要将共享空间数据复制为自己的私有空间数据后，再对私有空间数据进行重写。
   • 而标记-清除算法需要频繁的设置所有活动对象的头的标志位，这样就会频繁发生本不应该发生的复制，压迫到内存空间。

---

为了解决分配速度的问题, 人们提出了两种方法

1. 使用多个空闲链表（multiple free-list)

   • 类似于建立索引的方法。

   • 为了防止空闲链表（也就是索引）的数组过大的问题，通常会给分块大小设定一个上限。

   • 大于这个上限的按照一个空闲链表处理。

     • ex.
     • 设置上限为100
     • 那么准备1～100及大于等于101个字的100个空闲链表就可以了。

   -> 伪代码描述使用多个空闲链表的内存分配
   
   new_obj(size){
       index = size / (WORD_LENGTH / BYTE_LENGTH)
       if(index <= 100)
           if($free_list[index] != NULL)
               chunk = $free_list[index]
               return chunk
       else
           chunk = pickup_chunk(size, $free_list[101])
           if(chunk != NULL)
               return chunk
               
       allocation_fail() # 大招，销毁并释放全部空间
   }
   

   -> 伪代码描述使用多个空闲链表的内存合并
   
   sweep_phase() {
       for(i : 2...101)
           $free_list[i] = NULL
    
       sweeping = $heap_start
       
       while(sweeping < $heap_end)
           if(sweeping.mark == TRUE)
               sweeping.mark = FALSE
           else:
               index = size / (WROD_LENGTH / BYTE_LENGTH)
               if(index<=100)
                   sweeping.next = $free_list[index]
                   $free_list[index] = sweeping
               else
                   sweeping.next = $free_list[101]
                   $free_list[101] = sweeping
           sweeping += sweeping.size   
   }
   

2. BiBOP(Big Bag Of Pages)法

   • BiBOP法是指将大小相近的对象整理成固定大小的块进行管理的做法
   • 对此我们可以把堆分割成固定大小的块，让每个块只能配置同样大小的对象。

   

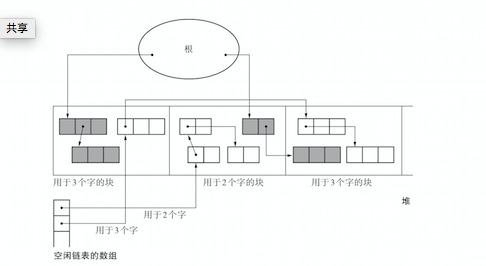
• 缺点
  BiBOP并不能完全消除碎片化。可能出现某一个块中活动对象过少的问题。

    比如在全部用于2个字的块中，只有一个活动对象
    BiBOP法原本是为了消除碎片化，提高堆的使用效率而采用的方法。
    但像上面这样，在多个块中分散残留着同样大小的对象，反而会降低堆的使用效率。
  

为了解决与写时复制不兼容的问题，则采取位图标记的方法

• 位图标记

  位图标记的方法就是只收集各个对象的标志位并表格化，不跟对象一起管理。在标记的时候，不在对象的头里标记，而是在这个表格中的标记。

  像这样集合了用于标记的位的表格称为“位图表格”。

  

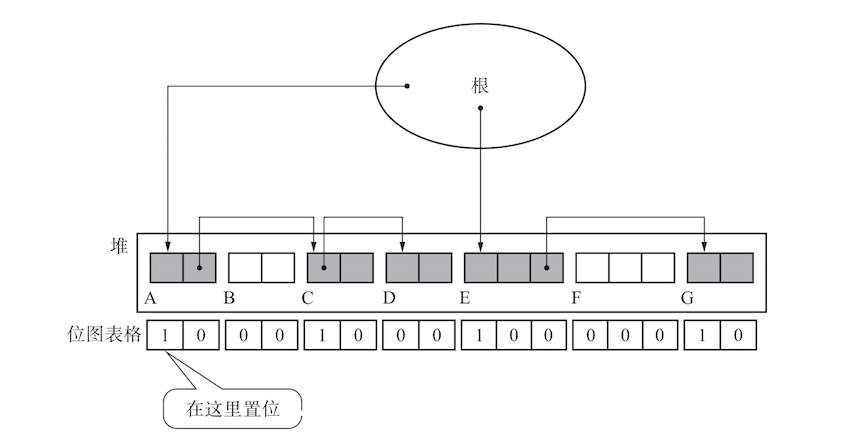
  • 优点

    1. 与写时复制技术兼容
    2. 清除操作更高效

  • 注意

    • 有多个堆的话，一班会为每个堆都准备一个位图表格

---

延迟清除法（Lazy Sweep）

延时清除法是缩减因清除操作而导致的mutator最大暂停时间的方法。在标记操作结束后，不立即进行清除操作。

-> 伪代码描述延时清除法中的分配操作

new_obj（size){
    chunk = lazy_sweep(size)
    if(chunk != NULL)
        reutrn chunk
    
    make_phase()
    
    chunk = lazy_sweep(size)
    if(chunk != NULL)
        return chunk
        
    allocation_fail()
}

lazy_sweep(size){
    while($sweeping < $heap_end)
        if($sweeping.mark == TRUE)
            $sweeping.mark == FALSE
        else if($sweeping.size >= size)
            chunk = $sweeping
            $sweeping += $sweeping.size
            return chunk
        $sweeping += $sweeping.size
    $sweeping = $heap_start
    return NULL
}

• lazy_sweep() 函数会一直遍历堆，知道找到大于等于所申请大小的分块为止。
• 在找到合适的分块时会将其返回。
• 但是在这里$sweeping 变量时全局变量。也就是说遍历的开始为止位于上一次清除操作中发现的分块的右边。
• 当lazy_sweep()函数遍历到堆的最后都没有找到分块时，会返回NULL。
• 因为延时清除法不是一下遍历整个堆，它只在分配时执行必要的遍历，所以可以压缩因清除操作而导致的mutator的暂停是时间。这就是“延时”清除操作的意思。

缺点

延时清除的效果是不均衡的

如图：



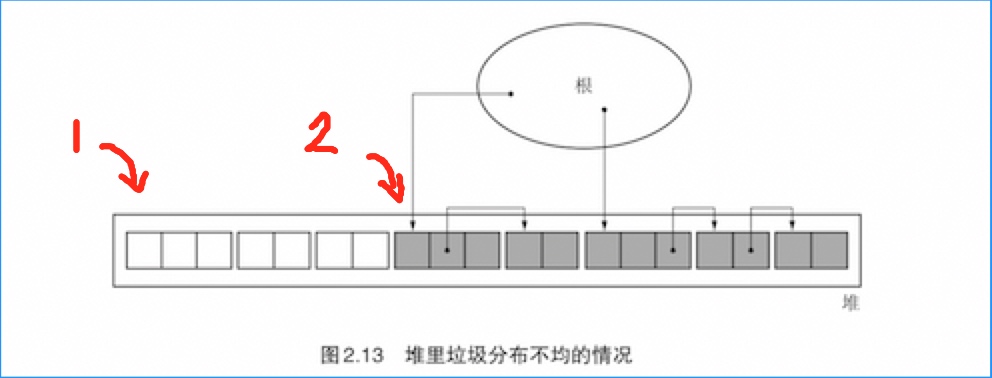
• 如果垃圾和活动对象在堆中的分布都变成连续的，那么程序在垃圾部分(1标示的位置)能马上获得分块。而一旦程序进入活动对象周围（2标示的位置），就怎么都无法获得分块了。这样就增加了mutator的暂停时间。