一、统计学习三要素
1.模型:要学习的条件概率分布或决策函数。模型的假设空间包含所有可能的条件概率分布或决策函数。例如:假设决策函数是输入变量的线性函数,那么模型的假设空间就是所有这些线性函数构成的函数集合,此时为无穷个。
这也就是为什么说:条件概率分布(P(y|x))和函数(y=f(x))可以相互转换。
条件概率分布最大化后得到函数:决策准则是最大可能性时,决策函数自然取条件概率的最大值。
函数归一化后得到条件概率分布:决策函数归一化之后满足概率公理,当然可以看作条件概率。决策函数的定义域通常是有限点集。
2. 策略:统计学习的目的是从假设空间中选取最优模型,需要损失函数和风险函数。
3. 算法:用什么样的算法求解最优模型。比如梯度下降
二、正则化的作用是选择经验风险与模型复杂度同时较小的模型
从贝叶斯估计角度看,正则化项对应于模型的先验概率。假设复杂的模型有较小的先验概率。简单的模型有较大的先验概率。
三、生成模型和判别模型
生成模型:由数据学习联合概率分布(P(X,Y)),然后求出条件概率分布(P(Y|X))作为预测的模型
[P(Y|X)=frac{P(X,Y)}{P(X)}
]
典型的生成模型:朴素贝叶斯,HMM.
判别模型:由数据直接学习决策函数(f(X))或者条件概率分布(P(Y|X))作为预测的模型。
典型的判别模型:k近邻,感知机,决策树,LR,SVM,条件随机场。
四、第一章习题
1.2通过经验风险最小化推导极大似然估计,证明模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化等价于极大似然估计。
经验风险最小化即求解下列最优化问题:
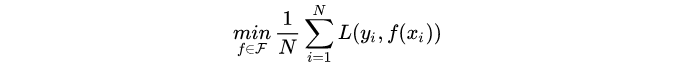
当模型是条件概率分布,损失函数是对数损失函数时,上述问题等价于:

考虑到N是常数,因此,上述上述问题又等价于:
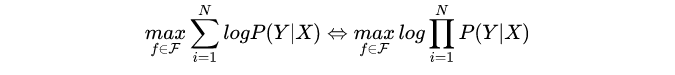
这就是极大似然估计。