左神算法之获取栈中最小值

设计一个能够获取当前栈最小值的栈

问题描述

​ 实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作，要求pop、push、getMin 操作的时间复杂度都是 O(1)。

解题思路

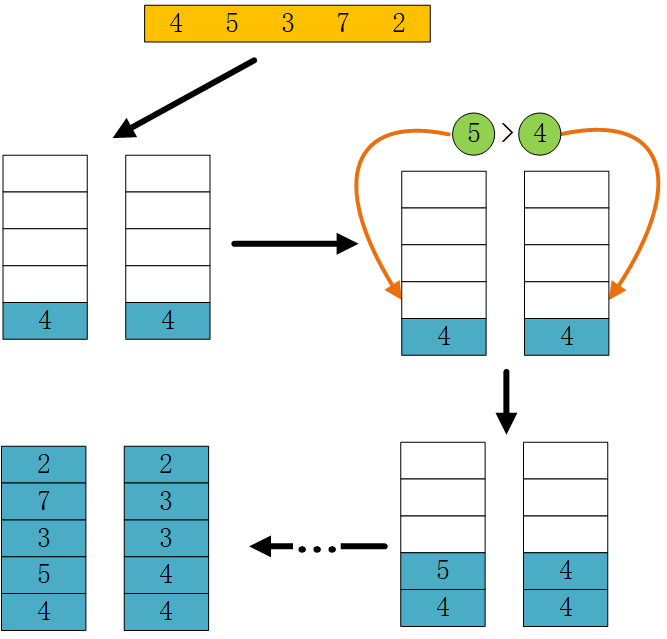
​ 使用两个栈来实现这一功能，一个普通栈stackData，一个能获取最小值的栈stackMin。

具体实现

1. 将当前数压入stackData中，设当前要压入值为newNum，直接压入stackData；
2. 将当前数压入stackMin中：
   • 判断最小栈stackMin是否有数，没有的话直接将数压栈；
   • 当普通栈stackData的数小于最小栈stackMin的数，直接将数压栈；
   • 若普通栈的数大于等于最小栈的数，将最小栈的栈顶元素再压一次进栈。
3. 将两个栈中的元素弹出，弹出规则正常弹出即可；
4. 获取最小值的方法，即返回最小值栈的栈顶

代码实现

public class TwoStack{
	//申请两个栈，一个普通栈stackData，
	//一个能获取最小值的栈stackMin(从栈底到栈顶依次减小的栈)
	public Stack<Integer> stackData;
    public Stack<Integer> stackMin;
	//初始化两个栈
    public TwoStack() {
        stackData = new Stack<Integer>();
        stackMin = new Stack<Integer>();
    }
	//两个栈各自的push方法，为了和栈的方法push区别开命名ppush
    public void ppush(int newNum){
		//stackData的push，直接将数压栈
        stackData.push(newNum);
		//判断最小栈是否有数，没有的话直接将数压栈
        if(stackMin.isEmpty()){
            stackMin.push(newNum);
		//当普通栈的数小于最小栈的数，直接将数压栈
		//比较的是每次要入栈的数和最小栈的栈顶元素
        }else if(newNum < this.getmin()){
            stackMin.push(newNum);
        }else{
		//若普通栈的数大于等于最小栈的数，将最小栈的栈顶元素再压一次进栈
            int newMin = stackMin.peek();
            stackMin.push(newMin);
        }
    }
	//两个栈各自的pop方法,为了和栈的方法pop区别开命名ppop
    public int ppop(){
        if(stackData.isEmpty()){
            throw new RuntimeException("普通栈空了");
        }
        stackMin.pop();
        return stackData.pop();
    }
	//获取最小值的方法，本质就是返回最小值栈的栈顶
    private int getmin() {
        if(stackMin.isEmpty()){
            throw new RuntimeException("最小数栈空了");
        }
        return stackMin.peek();
    }
}