前文:Lasso linear model实例 | Proliferation index | 评估单细胞的增殖指数
参考:LASSO回歸在生物醫學資料中的簡單實例 - 生信技能树
Linear least squares, Lasso,ridge regression有何本质区别?
你应该掌握的七种回归技术 (好文,解释了各个回归的特点,以及分别应用在什么场合)
热门数据挖掘模型应用入门(一): LASSO 回归 - 侯澄钧
Feature Selection using LASSO - 原文论文 (英文的讲解更全面,更好理解,强烈推荐阅读)
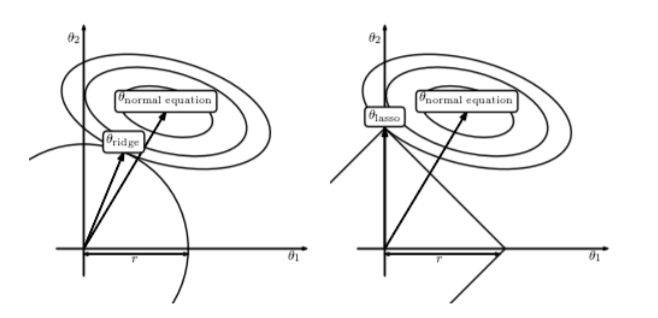
这幅图解释了为什么LASSO会让大部分的βj(λ) = 0
假设一个二维模型对应的系数是 β1 和 β2,然后 β 是最小化误差平方和的点, 即用传统线性回归得到的自变量系数。 但我们想让这个系数点必须落在蓝色的正方形内,所以就有了一系列围绕 β 的同心椭圆, 其中最先与蓝色正方形接触的点,就是符合约束同时最小化误差平方和的点。
两篇经典文章:
Prediction of clinical outcome in glioblastoma using a biologically relevant nine-microRNA signature
回归中的多重共线性 Multicollinearity
elastic net
sklearn.linear_model.LassoCV Python API
常识:
||w||_2: ||w||带一个下标2 的意思是这个该向量的范数为欧几里得范数,设w=<x1,x2,x3>, ||w||_2=x1^2+x2^2+x3^2 的开根号。
(||w||_2)^2 的意思是w的欧几里得范数的平方,也就是(||w||_2)^2=x1^2+x2^2+x3^2
ŷ:y的估计值
arg min 就是使后面这个式子达到最小值时的变量的取值
今天经同学指点才发现自己的认知问题,豁然开朗!!
在python sklearn里,L1就是Lasso,L2就是ridge!
所以Lasso就像是贝叶斯一样,只是附加到基础模型上的东西。
待续~