树上莫队学习笔记
前言
今天(19.7.12)A组第一题是一道树上莫队裸题
就学一下咯
参考
正文
前置知识
欧拉序
这里的欧拉序指的是每次进入和出节点都要把节点加进序列里
比如这个图:
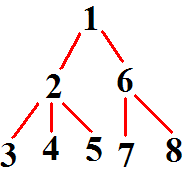
欧拉序就是:
1 2 3 3 4 4 5 5 2 6 7 7 8 8 6 1
进 进 进 出 进 出 进 出 出 进 进 出 进 出 出 出
(每个结点恰好出现了两次)
算法流程
各种树上问题有很多可以在树的某种遍历序列上乱搞。
树上莫队就是利用欧拉序把树上问题转化为序列上的问题。
既然在序列上就显然可以用普通莫队
设st[x]表示x这个节点第一次出现在序列中的位置,en[x]表示x这个节点最后出现在序列中的位置。
当我们想求树上x到y的贡献时,设st[x]<st[y]
1.当lca(x,y)=x时
x,y在一条链上,此时st[x]到st[y]这一段区间中出现过一次的点要加进答案里,出现两次的不统计。
2.当lca(x,y)!=x时
x,y在两个子树中。此时ed[x]到st[y]这一段区间中出现过一次的点要加进答案里,出现两次的不统计。
同时,这样子做会不统计lca,所以最后把lca临时加进答案里。
此处纯为作者瞎扯。。。
- 为什么出现两次的点不统计答案
树上路径的定义为:从x到y经过节点个数最少的路径。
若一个点k出现两次,说明我们可以先访问k,进入k的子树中,然后出来,再到y,很显然不访问k是更优的。因此出现两次的点不能统计入答案
- 为什么当lca(x,y)≠x时需要从ed[x]开始遍历
从st[x]到ed[x]为x的子树中的节点,很显然这些节点不能统计进答案注:这里我觉得是因为从st[x]开始算的话,x不会被统计进答案里(出现两次)
By 自为风月马前卒
实现的时候,维护一个bz数组表示bz[x]是在当前序列中出现了几次(%2)
每次标记移到新的节点x时判一下bz[x],再把bz[x]取反
例题
【GMOJ3360】苹果树
神犇家门口种了一棵苹果树。苹果树作为一棵树,当然是呈树状结构,每根树枝连接两个苹果,每个苹果都可以沿着一条由树枝构成的路径连到树根,而且这样的路径只存在一条。由于这棵苹果树是神犇种的,所以苹果都发生了变异,变成了各种各样的颜色。我们用一个1到N之间的正整数来表示一种颜色。树上一共有N个苹果。每个苹果都被编了号码,号码为一个1到N之间的正整数。我们用0代表树根。只会有一个苹果直接连到树根。
有许许多多的人来神犇家里膜拜神犇。可神犇可不是随便就能膜拜的。前来膜拜神犇的人需要正确回答一个问题,才能进屋膜拜神犇。这个问题就是,从树上编号为N的苹果出发,由树枝走到编号为N的苹果,路径上经过的苹果一共有多少种不同的颜色(包括苹果u和苹果v的颜色)?不过神犇注意到,有些来膜拜的人患有色盲症。具体地说,一个人可能会认为颜色a就是颜色b,那么他们在数苹果的颜色时,如果既出现了颜色a的苹果,又出现了颜色b的苹果,这个人只会算入颜色b,而不会把颜色a算进来。
神犇是一个好人,他不会强人所难,也就会接受由于色盲症导致的答案错误(当然答案在色盲环境下也必须是正确的)。不过这样神犇也就要更改他原先数颜色的程序了。虽然这对于神犇来说是小菜一碟,但是他想考验一下你。你能替神犇完成这项任务吗?
n<=50000m<=100000
树上莫队的裸题。
色盲的话,如果a和b都在的话,ans-=1就好了。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct qy
{
int x,y,z,l,r,lk,rank,ans,a,b;
};
int n,m,i,j,k,x,y,len,l,r,z,ans;
int a[400005];
int ll[400005],next[400005],last[100005],tot,depth[100005];
int fa[400005][20];
int list[400005],st[400005],en[400005];
qy q[400005];
int s[400005],bz[400005];
void insert(int x,int y)
{
tot++;
ll[tot]=y;
next[tot]=last[x];
last[x]=tot;
}
void build(int x)
{
list[++list[0]]=x;
st[x]=list[0];
for (int i=1;i<=19;i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for (int i=last[x];i>=1;i=next[i])
{
if (depth[ll[i]]==0)
{
depth[ll[i]]=depth[x]+1;
fa[ll[i]][0]=x;
build(ll[i]);
}
}
list[++list[0]]=x;
en[x]=list[0];
}
int lca(int x,int y)
{
if (depth[x]<depth[y]) swap(x,y);
for (int i=19;i>=0;i--)
{
if (depth[fa[x][i]]>=depth[y])
x=fa[x][i];
}
if (x==y) return x;
for (int i=19;i>=0;i--)
{
if (fa[x][i]!=fa[y][i])
{
x=fa[x][i];
y=fa[y][i];
}
}
return fa[x][0];
}
int comp(qy a,qy b)
{
return ((a.lk<b.lk)||((a.lk==b.lk)&&(a.r<=b.r)));
}
int compp(qy a,qy b)
{
return a.rank<b.rank;
}
void update(int x)
{
if (bz[x]==0)
{
if (s[a[x]]==0) ans++;
s[a[x]]++;
}
else
{
s[a[x]]--;
if (s[a[x]]==0) ans--;
}
bz[x]^=1;
}
int main()
{
freopen("read.in","r",stdin);
freopen("write.out","w",stdout);
len=440;
scanf("%d%d",&n,&m);
for (i=1;i<=n;i++)
scanf("%d",&a[i]);
for (i=1;i<=n;i++)
{
scanf("%d%d",&x,&y);
if ((x!=0)&&(y!=0))
{
insert(x,y);
insert(y,x);
}
}
depth[1]=1;
build(1);
for (i=1;i<=m;i++)
{
scanf("%d%d%d%d",&q[i].x,&q[i].y,&q[i].a,&q[i].b);
if (q[i].a==q[i].b)
q[i].a=q[i].b=0;
if (st[q[i].x]>st[q[i].y])
swap(q[i].x,q[i].y);
z=lca(q[i].x,q[i].y);
if (q[i].x==z)
{
q[i].l=st[q[i].x];
q[i].r=st[q[i].y];
q[i].lk=(q[i].l-1)/len+1;
}
else
{
q[i].l=en[q[i].x];
q[i].r=st[q[i].y];
q[i].lk=(q[i].l-1)/len+1;
}
q[i].rank=i;
q[i].z=z;
}
sort(q+1,q+1+m,comp);
l=r=0;
for (i=1;i<=m;i++)
{
while (r<q[i].r)
{
r++;
update(list[r]);
}
while (r>q[i].r)
{
update(list[r]);
r--;
}
while (l>q[i].l)
{
l--;
update(list[l]);
}
while (l<q[i].l)
{
if (l!=0)
update(list[l]);
l++;
}
if (q[i].x!=q[i].z)
{
update(q[i].z);
q[i].ans=ans;
update(q[i].z);
}
else
{
q[i].ans=ans;
}
if ((s[q[i].a]>0)&&(s[q[i].b]>0))
{
q[i].ans--;
}
}
sort(q+1,q+1+m,compp);
for (i=1;i<=m;i++)
{
printf("%d
",q[i].ans);
}
}