堆排序
参考《算法导论》《C程序设计语言》
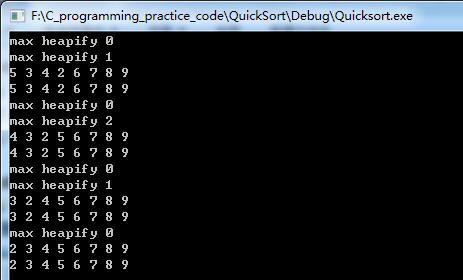
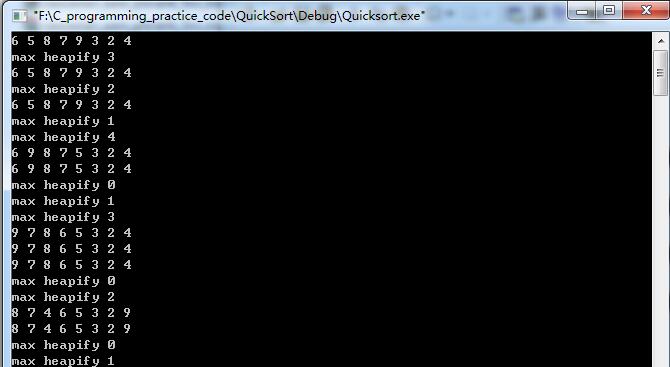
#include<stdio.h> int HEAPSIZE=8; int LENGTH=8; void view(int A[]); int parent(int i){//节点i的父节点下标 return (i+1)/2-1; } int left(int i){//节点i的左孩子下标 return (i+1)*2-1; } int right(int i){//节点i的右孩子下标 return (i+1)*2; } void exchange(int A[], int i, int j){ int temp=A[i]; A[i]=A[j]; A[j]=temp; } //维护最大堆的性质A[parent[i]]>=A[i] void maxHeapify(int A[], int i){ printf("max heapify %d ",i); int l=left(i); int r=right(i); int largest; if((l<=(HEAPSIZE-1))&&(A[l]>A[i])) largest=l; else largest=i; if((r<=(HEAPSIZE-1))&&(A[r]>A[largest])) largest=r; if(largest!=i){ exchange(A,i,largest); //在交换后,下标为largest的节点是原来的A[i], 于是以该结点为根的 //子树有可能违反最大堆的性质 maxHeapify(A,largest); } view(A); } //用自底向上的方法把一个大小为n的数组A[0..n-1]转换为最大堆 void buildMaxHeap(int A[]){ for(int i=(LENGTH/2-1); i>=0; i--){ maxHeapify(A,i); } } //堆排序算法 void heapSort(int A[]){ buildMaxHeap(A); for(int i=LENGTH-1; i>=1; i--){ exchange(A,0,i); HEAPSIZE=HEAPSIZE-1; maxHeapify(A,0); } } int main(){ int A[8]={6,5,8,7,9,3,2,4}; view(A); heapSort(A); view(A); getchar(); getchar(); return 0; } void view(int A[]){//显示A数组当前状态 for(int i=0;i<8;i++){ putchar(A[i]+'0'); putchar(' '); } putchar(' '); }
实验结果
...