P中值选址问题的整数规划求解

P中值选址问题的整数规划求解

一 、P-中值问题

p-中值选址问题是一个常见的选址问题. 问题是给定I个需求结点和J个待选设施地点, 要求选择p个地点建立设施, 使得运输成本最低. 下面是个英文的问题详细描述: 

 二、整数规划模型

 p-中值选址问题的整数规划模型如下

 

 

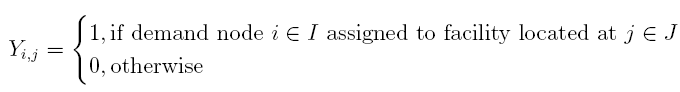
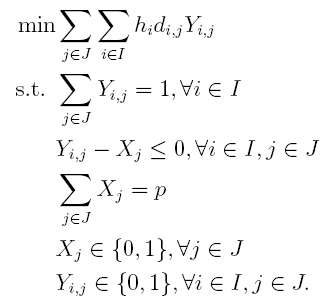
 三、当给定距离时候的求解

假设给定了设施-需求之间的距离矩阵，照着上面的模型即可写出Leapms模型。

//==========================================================
//The P-Median Problem
//==========================================================
min sum{j=1,...,J;i=1,...,I}h[i]d[i][j]y[i][j]
subject to
    sum{j=1,...,J}y[i][j]=1|i=1,...,I
    y[i][j]-x[j]<=0|i=1,...,I;j=1,...,J
    sum{j=1,...,J}x[j]=p
where
    I,J are numbers
    p is a number
    h is a set
    d[i][j] is a number | i=1,...,I;j=1,...,J
    x[j] is a variable of binary|j=1,...,J
    y[i][j] is a variable of binary|i=1,...,I;j=1,...,J

data
    I=10
    J=10
    p=6
    h={3.1,2.2,4.3,5.0,7.1,8.0,9.9,3.4,4.3,3.3}
    d={
        73 30 15  8 67 34 82 50  9 12
        89 85 90 56 79 51 52 72 51 52
        26 99 60 47 47 21 20 30 42 27
        97 99 89 60 96 43  2  7 45 34
        27 46 34 54 61 97 12 55 39 23
        73 46 81 12 15 44 46 76 48 36
         6 60 31 47 41  8 34 69 57 23
        46  5 45 37 14 75 72 12 15 88
        42 10 93 36 19 63 71 42 94 62
        62 44 66 11 88 81 52 42 81 43
    }

把上面的模型保存为pemedian1.leap

在leapms中求解： 依次输入load, pmedian1, mip即可求解

。。。 。。。

 

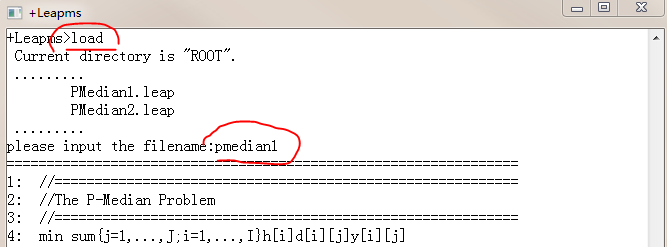
 四、当给定设施和需求点坐标时候的求解

与上面类似，不过设施和需求点的距离需要用data_relation 段用公式表达出来，leapms表达的模型如下

//==========================================================
//The P-Median Problem
//==========================================================
min sum{j=1,...,J;i=1,...,I}h[i]d[i][j]y[i][j]

subject to

	sum{j=1,...,J}y[i][j]=1|i=1,...,I
	y[i][j]-x[j]<=0|i=1,...,I;j=1,...,J
	sum{j=1,...,J}x[j]=p

where
	I,J are numbers
	p is a number
	h is a set

	cdx1[i],cdy1[i] are numbers|i=1,...,I
	cdx2[j],cdy2[j] are numbers|j=1,...,J

	d[i][j] is a number | i=1,...,I;j=1,...,J
	x[j] is a variable of binary|j=1,...,J
	y[i][j] is a variable of binary|i=1,...,I;j=1,...,J

data_relation

	d[i][j]=sqrt((cdx1[i]-cdx2[j])^2+(cdy1[i]-cdy2[j])^2)|-->
		i=1,...,I;j=1,...,J
data
	I=10
	J=10

	p=6
	h={3.1, 2.2, 4.3, 5.0, 7.1, 8.0, 9.9, 3.4, 4.3, 3.3}

	cdx1={-9.7, 8.8,8.3,7.1,-6.8, 6.7,-5.8,0.7,7  , -6  }
	cdy1={-8.3,-1.9,-0.1,-3, 4 , -4.1, 4.4,2.5,4.4,  8.8}

	cdx2={-1.9,-8.3,2.5,0.8,-2.2, 4.1,-1.2,9.2,-0.9,1}
	cdy2={-6.6,-0.9,1  ,8.2, 0.5,-8.9,-2.2,9.5,-4  ,6}

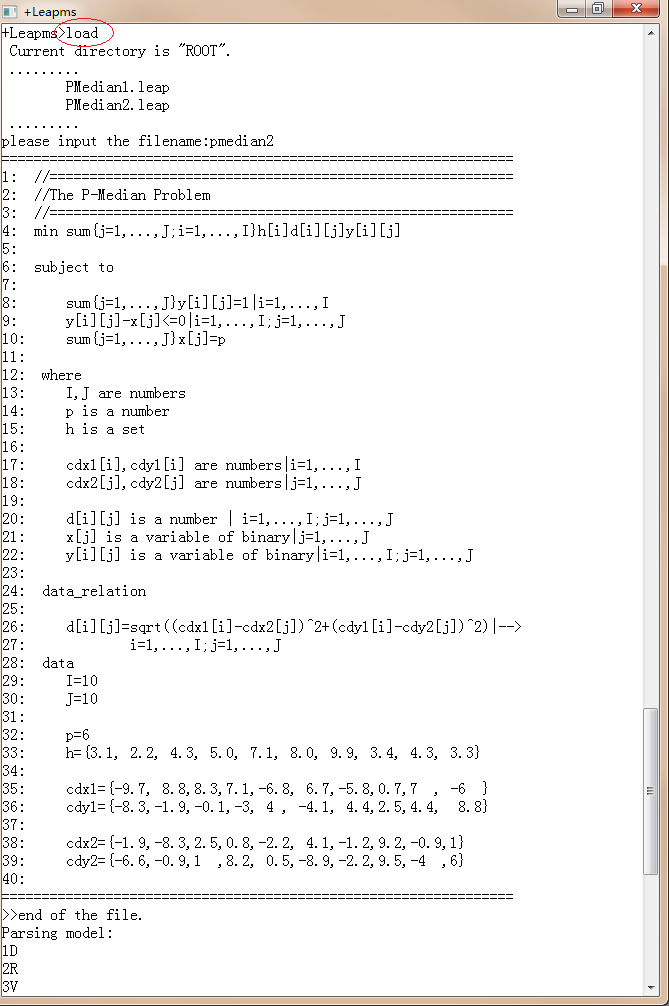
把上面的模型保存为pemedian2.leap

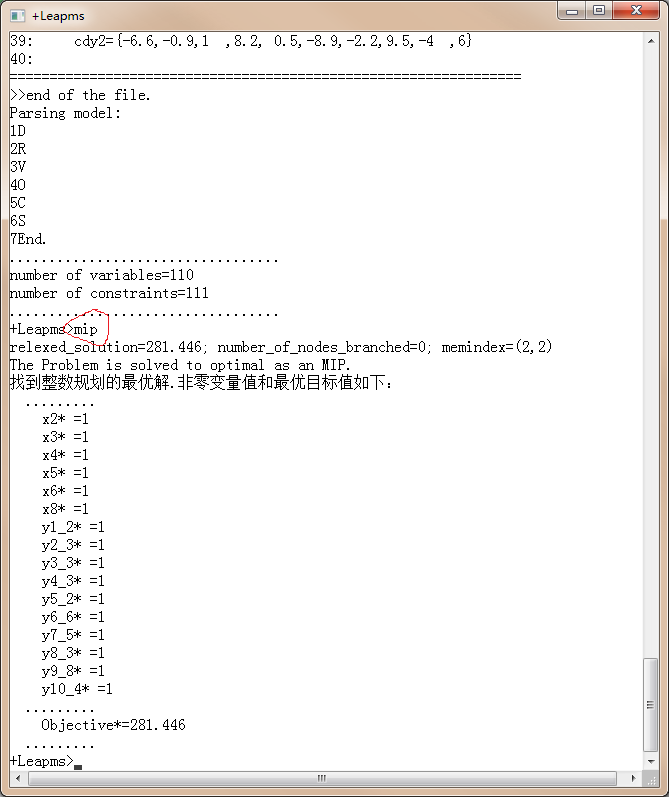
在leapms中求解： 依次输入load, pmedian2, mip即可求解