题目
有一个二维矩阵 grid ,每个位置要么是陆地(记号为 0 )要么是水域(记号为 1 )。
我们从一块陆地出发,每次可以往上下左右 4 个方向相邻区域走,能走到的所有陆地区域,我们将其称为一座「岛屿」。
如果一座岛屿 完全 由水域包围,即陆地边缘上下左右所有相邻区域都是水域,那么我们将其称为 「封闭岛屿」。
请返回封闭岛屿的数目。
示例 1:
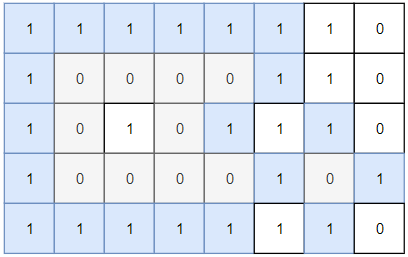
输入:grid = [[1,1,1,1,1,1,1,0],
[1,0,0,0,0,1,1,0],
[1,0,1,0,1,1,1,0],
[1,0,0,0,0,1,0,1],
[1,1,1,1,1,1,1,0]]
输出:2
解释:
灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
示例 2:

输入:grid = [[0,0,1,0,0],
[0,1,0,1,0],
[0,1,1,1,0]]
输出:1
示例 3:
输入:grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出:2
提示:
1 <= grid.length, grid[0].length <= 100
0 <= grid[i][j] <=1
解答
本题与岛屿数量的区别在于和边界相连的岛屿不算岛屿。从某个点开始深搜是否会连接到边界,用一个变量标记即可
color对每次深搜标记,Time: O(mn), Space: O(mn)
(用广搜也可以做,大部分情况下,深度优先和广度优先可以相互替换。)
class Solution:
def __init__(self):
self.a = []
self.next = [
[0, 1],
[1, 0],
[0, -1],
[-1, 0]
]
self.m = 0
self.n = 0
self.p = 0 # 标记是否会连到边界
def closedIsland(self, grid) -> int:
if not grid:
return 0
self.a, self.m, self.n = grid, len(grid), len(grid[0])
color = 0
for i in range(1, self.m-1): # 不包含边界遍历
for j in range(1, self.n-1):
if self.a[i][j] == 0:
self.p = 0
color -= 1
self.a[i][j] = color
self.dfs(i, j, color)
if self.p != 0:
color += 1
return -color
def dfs(self, x, y, color):
for i in range(4):
tx = x + self.next[i][0]
ty = y + self.next[i][1]
if tx >= 0 and ty >= 0 and tx < self.m and ty < self.n and self.a[tx][ty] == 0:
if tx == 0 or ty == 0 or tx == self.m-1 or ty == self.n-1: # 与边界相连
self.p = 1
else:
self.a[tx][ty] = color
self.dfs(tx, ty, color)
s = Solution()
ans = s.closedIsland([
[0, 0, 1, 1, 0, 1, 0, 0, 1, 0],
[1, 1, 0, 1, 1, 0, 1, 1, 1, 0],
[1, 0, 1, 1, 1, 0, 0, 1, 1, 0],
[0, 1, 1, 0, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 0, 0, 1, 1, 1, 0],
[0, 1, 0, 1, 0, 1, 0, 1, 1, 1],
[1, 0, 1, 0, 1, 1, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 0, 0, 0, 0],
[1, 1, 1, 0, 0, 1, 0, 1, 0, 1],
[1, 1, 1, 0, 1, 1, 0, 1, 1, 0]
])
print(ans)
# # 染色后的矩阵
# import pprint
# pprint.pprint(s.a)
# 5
# [[0, 0, 1, 1, 0, 1, 0, 0, 1, 0],
# [1, 1, -1, 1, 1, -2, 1, 1, 1, 0],
# [1, -2, 1, 1, 1, -2, -2, 1, 1, 0],
# [0, 1, 1, -2, -2, -2, -2, 1, -3, 1],
# [0, -2, -2, -2, -2, -2, 1, 1, 1, 0],
# [0, 1, -2, 1, -2, 1, -4, 1, 1, 1],
# [1, -4, 1, -5, 1, 1, -4, -4, -4, 1],
# [1, 1, 1, 1, 1, 1, -4, -4, -4, 0],
# [1, 1, 1, -6, -6, 1, -4, 1, -4, 1],
# [1, 1, 1, 0, 1, 1, 0, 1, 1, 0]]