Xor Sum(讲解异或)【字典树】

Xor Sum

题目链接(点击)

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 132768/132768 K (Java/Others)
Total Submission(s): 6182    Accepted Submission(s): 2683

Problem Description

Zeus 和 Prometheus 做了一个游戏，Prometheus 给 Zeus 一个集合，集合中包含了N个正整数，随后 Prometheus 将向 Zeus 发起M次询问，每次询问中包含一个正整数 S ，之后 Zeus 需要在集合当中找出一个正整数 K ，使得 K 与 S 的异或结果最大。Prometheus 为了让 Zeus 看到人类的伟大，随即同意 Zeus 可以向人类求助。你能证明人类的智慧么？

Input

输入包含若干组测试数据，每组测试数据包含若干行。
输入的第一行是一个整数T（T < 10），表示共有T组数据。
每组数据的第一行输入两个正整数N，M（<1=N,M<=100000），接下来一行，包含N个正整数，代表 Zeus 的获得的集合，之后M行，每行一个正整数S，代表 Prometheus 询问的正整数。所有正整数均不超过2^32。

Output

对于每组数据，首先需要输出单独一行”Case #?:”，其中问号处应填入当前的数据组数，组数从1开始计算。
对于每个询问，输出一个正整数K，使得K与S异或值最大。

Sample Input

2
3 2
3 4 5
1
5
4 1
4 6 5 6
3

Sample Outpu
Case #1:

4

3

Case #2:

4

思路：

1.题目要求异或最大值：异或（简单说就是没有进位的求和位运算）

例如：                           3      ⊕     5

分别用二进制表示：   1 1          1 0 1 

将他们相加：        结果为（110）2=（6）10

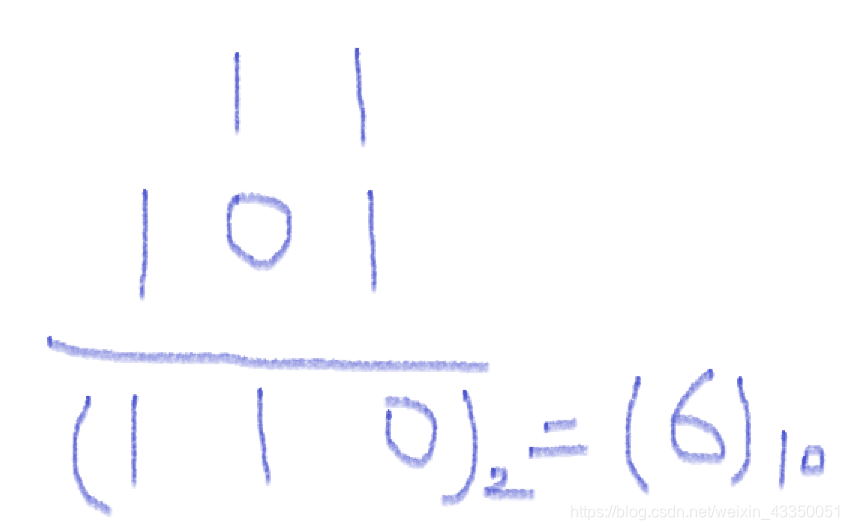
计算机计算异或代码：

#include<stdio.h>
int main()
{
    int a,b;
    scanf("%d%d",&a,&b);
    int sum=a^b;
    printf("%d
",sum);
    return 0;
}

2.在输入的时候会给出一个值n让去找一个异或结果最大的值

根据上面介绍异或也可以看出来 要想使异或结果最大那就应该尽力去寻找与n的二进制 相反的值

例如5的二进制是101 那就应该寻找010即2这个数与其异或 

但是2未必一定是之前输入过的 所以尽可能寻找与2的二进制相似的值 比如 101 或 001 ...

3.最后就是

用字典树将之前输入的值的二进制存入 然后根据2中的方法寻找异或结果最大的数

4.还有个问题就是之前做过 几道类似的求异或结果最大的题目 但之前没使用位运算求二进制然后存入字典树中但也AC了

后来导致这个题目用原来的方法错误 仔细找了找才发现是因为我存数组的时候的问题：

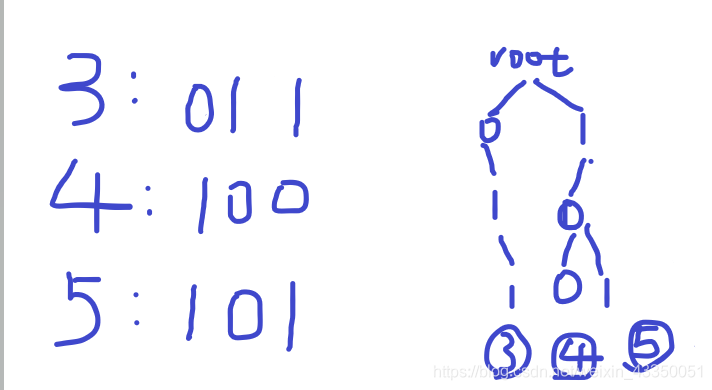
这种方法是错误的 之前对也是侥幸 正确的方法如下：（先将3的位数补够3位然后存入字典树）

 

AC代码：

#include<stdio.h>
#include<string.h>
typedef long long LL;
const int MAX=2e6;
LL n,m;
LL a[MAX+5],b[MAX+5];
LL top;
LL tir[MAX+5][2],num[MAX+5];
void insert(LL *b)
{
    LL root=0;
    for(LL i=31;i>=0;i--){
       // printf("*%d ",b[i]);
        LL id=b[i]-0;
        if(tir[root][id]==0){
            tir[root][id]=++top;
        }
        root=tir[root][id];
    }
    //printf("
");

}
LL find(LL *b)
{
    LL root=0;
    for(LL i=31;i>=0;i--){
      //  printf("*%d ",b[i]);
        LL id=b[i]-0;
        if(tir[root][id]==0){
            id==0?id=1:id=0;
        }
        if(tir[root][id]==0){
            break;
        }
        num[i]=id;
        root=tir[root][id];
    }
   // printf("
");
    LL sum2=0;
    LL sum1=1;
    for(LL i=0;i<=31;i++){
      //  printf("*%d ",num[i]);
        sum2+=num[i]*sum1;
        sum1*=2;
    }
    //printf("
");
    return sum2;
}
void allbegin()
{
    for(int i=0;i<=top+10;i++){
        for(int j=0;j<=2;j++){
            tir[i][j]=0;
        }
    }
    //memset(tir,0,sizeof(tir));
    top=0;
}
int main()
{
    LL T;
    scanf("%lld",&T);
    for(LL k=1;k<=T;k++){
        scanf("%lld%lld",&n,&m);
        allbegin();
        for(LL i=0;i<n;i++){
            scanf("%lld",&a[i]);
            for(LL j=31;j>=0;j--){
                b[j]=((1<<j)&a[i])?1:0;
            }
            insert(b);
        }
        for(LL i=0;i<m;i++){
            scanf("%lld",&a[i]);
        }
        printf("Case #%lld:
",k);
        for(LL i=0;i<m;i++){
            for(LL j=31;j>=0;j--){
                LL u=((1<<j)&a[i])?1:0;
                if(u==0){
                    b[j]=1;
                }
                else{
                    b[j]=0;
                }
            }
            LL sum=find(b);
            printf("%lld
",sum);
        }
    }
    return 0;
}