过了这么久才来写博客,也是我这么一段时间都很低迷吧。。。。
老实来说,今年应该是要打提高组的。。。可还是打了普及组。。。
其实最猥琐的还是我连普及都写挂了,作为一个学了两年的人,图论,进阶dp都写过的人,才打了210分,我实在没脸。
现在来讲讲题解吧。
T1成绩
题目描述
牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:
总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%
牛牛想知道,这门课程自己最终能得到多少分。
输入输出格式
输入格式:
输入文件只有1行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。相邻两个数之间用一个空格隔开,三项成绩满分都是100分。
输出格式:
输出文件只有1行,包含一个整数,即牛牛这门课程的总成绩,满分也是100分。
输入输出样例
说明
输入输出样例1说明
牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
输入输出样例2说明
牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
数据说明
对于30%的数据,A=B=0。
对于另外30%的数据,A=B=100。
对于100%的数据,0≤A、B、C≤100且A、B、C都是10的整数倍。
1 #include<cstdio> 2 int n,m,k; 3 int main() 4 { 5 scanf("%d%d%d",&n,&m,&k); 6 printf("%d",n*2/10+m*3/10+k*5/10); 7 }
没达到我可以去吃**了
T2图书管理员
题目描述
图书馆中每本书都有一个图书编码,可以用于快速检索图书,这个图书编码是一个 正整数。 每位借书的读者手中有一个需求码,这个需求码也是一个正整数。如果一本书的图 书编码恰好以读者的需求码结尾,那么这本书就是这位读者所需要的。 小 D 刚刚当上图书馆的管理员,她知道图书馆里所有书的图书编码,她请你帮她写 一个程序,对于每一位读者,求出他所需要的书中图书编码最小的那本书,如果没有他 需要的书,请输出-1。
输入输出格式
输入格式:输入文件的第一行,包含两个正整数 n 和 q,以一个空格分开,分别代表图书馆里 书的数量和读者的数量。
接下来的 n 行,每行包含一个正整数,代表图书馆里某本书的图书编码。
接下来的 q 行,每行包含两个正整数,以一个空格分开,第一个正整数代表图书馆 里读者的需求码的长度,第二个正整数代表读者的需求码。
输出格式:输出文件有 q 行,每行包含一个整数,如果存在第 i 个读者所需要的书,则在第 i 行输出第 i 个读者所需要的书中图书编码最小的那本书的图书编码,否则输出-1。
输入输出样例
说明
【数据规模与约定】
对于 20%的数据,1 ≤ n ≤ 2。
另有 20%的数据,q = 1。
另有 20%的数据,所有读者的需求码的长度均为 1。
另有 20%的数据,所有的图书编码按从小到大的顺序给出。
对于 100%的数据,1 ≤ n ≤ 1,000,1 ≤ q ≤ 1,000,所有的图书编码和需求码均 不超过 10,000,000。
题解:
1 k[1]=10; 2 for(int i=2;i<=9;i++) 3 k[i]=k[i-1]*10;
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 int n,m,k[11],z,ans,a[1001],b[1001],c[1001]; 5 int main() 6 { 7 scanf("%d%d",&n,&m); 8 for(int i=1;i<=n;i++) 9 scanf("%d",&a[i]); 10 for(int i=1;i<=m;i++) 11 scanf("%d%d",&b[i],&c[i]); 12 k[1]=10; 13 for(int i=2;i<=9;i++) 14 k[i]=k[i-1]*10; 15 for(int i=1;i<=m;i++) 16 { 17 ans=1999999999; 18 for(int j=1;j<=n;j++) 19 { 20 int x=a[j]%k[b[i]]; 21 if(x==c[i]) 22 ans=min(a[j],ans); 23 } 24 if(ans==1999999999)printf("-1 "); 25 else 26 printf("%d ",ans); 27 } 28 }
T3棋盘
题目描述
有一个m × m的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 1 个金币。
另外, 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入输出格式
输入格式:数据的第一行包含两个正整数 m, n,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的 n 行,每行三个正整数 x, y, c, 分别表示坐标为( x, y)的格子有颜色 c。
其中 c=1 代表黄色, c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为( 1, 1),右下角的坐标为( m, m)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是( 1, 1) 一定是有颜色的。
输出格式:输出一行,一个整数,表示花费的金币的最小值,如果无法到达,输出-1。
输入输出样例
说明
输入输出样例 1 说明
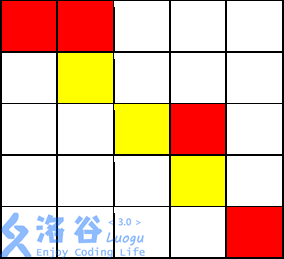
从( 1, 1)开始,走到( 1, 2)不花费金币
从( 1, 2)向下走到( 2, 2)花费 1 枚金币
从( 2, 2)施展魔法,将( 2, 3)变为黄色,花费 2 枚金币
从( 2, 2)走到( 2, 3)不花费金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)走到( 3, 4)花费 1 枚金币
从( 3, 4)走到( 4, 4)花费 1 枚金币
从( 4, 4)施展魔法,将( 4, 5)变为黄色,花费 2 枚金币,
从( 4, 4)走到( 4, 5)不花费金币
从( 4, 5)走到( 5, 5)花费 1 枚金币
共花费 8 枚金币。
输入输出样例 2 说明
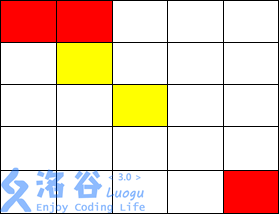
从( 1, 1)走到( 1, 2),不花费金币
从( 1, 2)走到( 2, 2),花费 1 金币
施展魔法将( 2, 3)变为黄色,并从( 2, 2)走到( 2, 3)花费 2 金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)只能施展魔法到达( 3, 2),( 2, 3),( 3, 4),( 4, 3)
而从以上四点均无法到达( 5, 5),故无法到达终点,输出-1
数据规模与约定
对于 30%的数据, 1 ≤ m ≤ 5, 1 ≤ n ≤ 10。
对于 60%的数据, 1 ≤ m ≤ 20, 1 ≤ n ≤ 200。
对于 100%的数据, 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 int n,m,ans,x,y,z,nex,mp[101][101],f[101][101],Sum=999999999,dx[4]={0,0,1,-1},dy[4]={1,-1,0,0}; 6 void dfs(int x,int y,int s) 7 { 8 for(int i=0;i<4;i++) 9 { 10 int nx=x+dx[i],ny=y+dy[i]; 11 if(nx<1||ny>n||nx>n||ny<1)continue; 12 if(mp[nx][ny]!=0) 13 { 14 if(mp[x][y]==0) 15 { 16 if(s==mp[nx][ny]) 17 { 18 if(f[nx][ny]>f[x][y]) 19 f[nx][ny]=f[x][y],dfs(nx,ny,mp[x][y]); 20 } 21 else 22 if(f[nx][ny]>f[x][y]+1) 23 f[nx][ny]=f[x][y]+1,dfs(nx,ny,mp[x][y]); 24 } 25 else 26 { 27 if(mp[x][y]==mp[nx][ny]) 28 { 29 if(f[nx][ny]>f[x][y]) 30 f[nx][ny]=f[x][y],dfs(nx,ny,mp[x][y]); 31 } 32 else 33 if(f[nx][ny]>f[x][y]+1) 34 f[nx][ny]=f[x][y]+1,dfs(nx,ny,mp[x][y]); 35 } 36 } 37 else 38 { 39 if(mp[x][y]==0)continue; 40 if(f[nx][ny]>=f[x][y]+2) 41 f[nx][ny]=f[x][y]+2,dfs(nx,ny,mp[x][y]); 42 } 43 } 44 } 45 int main() 46 { 47 scanf("%d%d",&n,&m); 48 for(int i=1;i<=m;i++) 49 scanf("%d%d%d",&x,&y,&z),mp[x][y]=z+1; 50 memset(f,127,sizeof(f)); 51 f[1][1]=0; 52 dfs(1,1,1); 53 if(f[n][n]!=2139062143) 54 printf("%d",f[n][n]); 55 else 56 printf("-1"); 57 }