
黑白染色,二分图
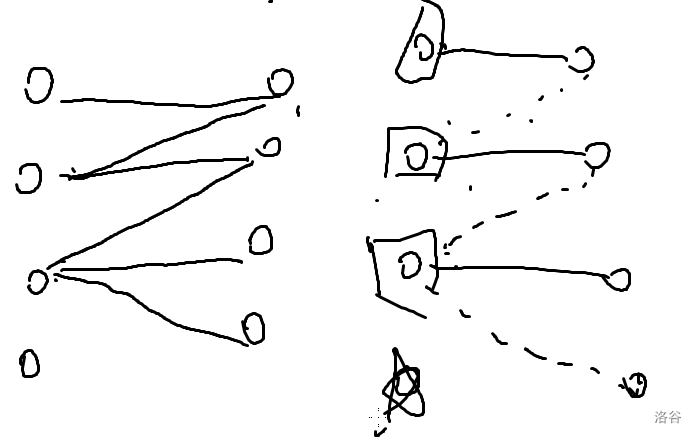
所有在最大匹配里面的点是必胜点?
不是,比如右边第三个点
那么在最大匹配里面有一些点是必胜点
结论是:必胜点一定在所有的最大匹配里面
证明:
如果小葱沿着匹配边走到了一个匹配点,分两种情况
如果大葱一直走匹配点,大葱必败
如果大葱走不在最大匹配里面的点,意味着小葱选择的点不是唯一的最大匹配点
所以选择所有的最大匹配点的公共点一定必胜
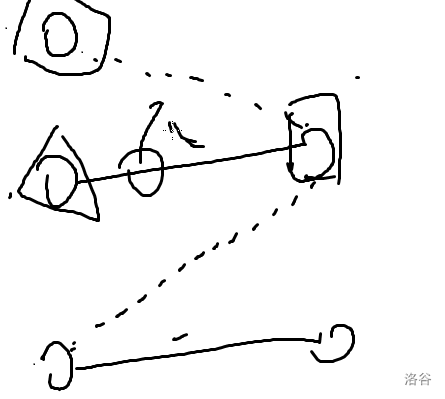
下面证选择不在最大匹配的点一定必败
则小葱走到的点一定是匹配点,这个时候一定是大葱必胜
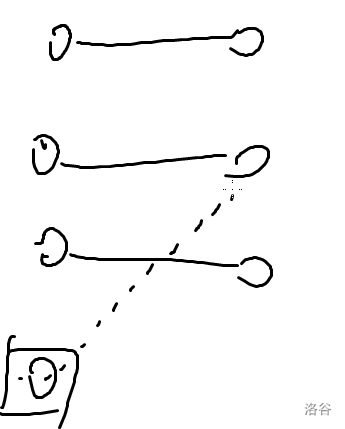
怎么判断一个点是否一定在二分图最大匹配里面?
如果把每个点删掉在跑,显然会炸
在匈牙利匹配的时候让一个点匹配的点再找一个匹配点,如果对应的点不能找到另一个匹配,那么这个点就一定在最大匹配里面
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
const int maxn=510;
const int maxp=maxn*maxn;
int n,m,k,en,id[maxn][maxn],result[maxp],bx[5]={0,1,-1,0,0},by[5]={0,0,0,1,-1};
bool block[maxn][maxn],use[maxp];
struct edge
{
int e;
edge *next;
}*v[maxp],ed[maxp*4];
void add_edge(int s,int e)
{
en++;
ed[en].next=v[s];v[s]=ed+en;v[s]->e=e;
}
bool dfs(int p)
{
for (edge *e=v[p];e;e=e->next)
if (!use[e->e])
{
use[e->e]=true;
if (!result[e->e] || dfs(result[e->e]))
{
result[e->e]=p;
result[p]=e->e;
return true;
}
}
return false;
}
bool dfs2(int p)
{
for (edge *e=v[p];e;e=e->next)
if (!use[e->e])
{
use[e->e]=true;
if (!result[e->e] || dfs2(result[e->e])) return true;
}
return false;
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
if (k==0)
{
if (n*m%2==1) printf("%d
",n*m/2);
else printf("%d
",n*m);
return 0;
}
for (int a=1;a<=k;a++)
{
int x,y;
scanf("%d%d",&x,&y);
block[x][y]=true;
}
int cnt=0;
for (int a=1;a<=n;a++)
for (int b=1;b<=m;b++)
if (!block[a][b]) id[a][b]=++cnt;
for (int a=1;a<=n;a++)
for (int b=1;b<=m;b++)
if (!block[a][b])
for (int c=1;c<=4;c++)
{
int x=a+bx[c];
int y=b+by[c];
if (!block[x][y] && x<=n && x>=1 && y<=m && y>=1) add_edge(id[a][b],id[x][y]);
}
int ans=0;
for (int a=1;a<=n;a++)
for (int b=1;b<=m;b++)
if ((a+b)&1)
{
if (block[a][b]) continue;
memset(use,false,sizeof(use));
if (dfs(id[a][b])) ans++;
}
for (int a=1;a<=cnt;a++)
result[result[a]]=a;
int res=0;
for (int a=1;a<=cnt;a++)
if (result[a])
{
memset(use,false,sizeof(use));
use[a]=true;
result[result[a]]=0;
if (!dfs2(result[a])) res++;
result[result[a]]=a;
}
printf("%d
",res);
return 0;
}