树链剖分

树链剖分

前置知识：线段树

树链剖分主要解决的是树上的操作，具体实现方法是把树上的操作变成对区间的操作。

先定义几个东西

树链：不拐弯的路径

重儿子：子树大小最大的子节点

重链：从一点出发，一直选择重儿子向下走，走到叶子节点

轻边：不属于任何一条重链的边

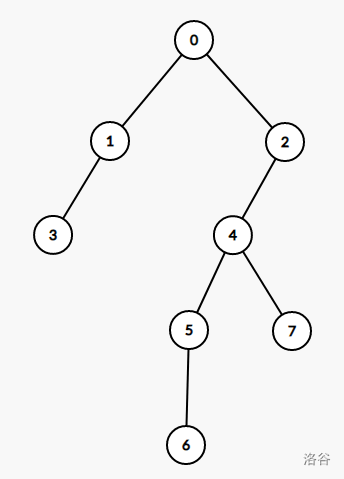
如图：对于节点(0)来说，他的重儿子是节点(2)，因为(2)的子树最大。他所在的重链是(0-2-4-5-6)

树链剖分，即把一条重链上的点放在一个连续的区间里面构成一个序列。比如上图剖玩以后有三条链，(0-2-4-5-6)，(1-3)，(7)，这样在对路径或者子树操作的时候就可以转化为序列的区间操作了。树上路径由(O(logN))个区间组成。

树剖的核心是两遍(dfs)，其中第一遍处理子树大小和重儿子，第二遍剖出重链

第一遍：

int fa[N];//父亲节点 
int dep[N];//节点深度 
int siz[N];//子树大小 
int son[N];//重儿子
void dfs1(int u, int f)
{
	son[u] = 0;
	siz[u] = 1;
	fa[u] = f;
	dep[u] = dep[f] + 1;
	for(int i = head[u]; i; i = edg[i].nxt)
	{
		int v = edg[i].to;
		if(v != f)
		{
			dfs1(v, u);
			siz[u] += siz[v];
			if(siz[v] > siz[son[u]]) son[u] = v;//处理重儿子
		}
	}
}

第二遍：

int dfn[N];//时间戳 
int top[N];//这个点所在重链的顶端节点 
int w[N];//新建序列的值 
int val[N];//原来节点的值 
void dfs2(int u, int f)
{
	dfn[u] = ++tim;
	w[tim] = val[u];//把原来节点和序列中元素对应 
	if(son[f] == u) top[u] = top[f];//重儿子所在重链的顶端节点和他父亲所在重链的顶端节点一个 
	else top[u] = u;//自己作为重链的顶端节点 
	if(son[u]) dfs2(son[u], u);//优先dfs重链，保证区间连续 
	for(int i = head[u]; i; i = edg[i].nxt)
	{
		int v = edg[i].to;
		if(v != f && v != son[u]) dfs2(v, u);//dfs其他儿子 
	}
}

查询两个节点之间路径的值：实质就是找两个节点的(LCA)，处理(LCA)到两个节点的信息。

首先如果这两个节点在同一条重链上，这两个点之间的区间一定是连续的，直接查询就好了。

否则每次找(top)的深度节点较大的节点，统计(top)到这一节点的信息，然后跳到(top)的父亲，重复操作

int querysum(int u, int v)
{
	int ans = 0;
	while(top[u] != top[v])//不在一条重链上 
	{
		if(dep[top[u]] < dep[top[v]]) swap(u, v);//找顶端节点深度较大的 
		ans += query1(1, 1, n, dfn[top[u]], dfn[u]);
		u = fa[top[u]];
	}//在同一条重链上 
	if(dfn[u] > dfn[v]) swap(u, v);
	ans += query1(1, 1, n, dfn[u], dfn[v]);
	return ans;
}

一道例题

P2590 [ZJOI2008]树的统计

甚至连懒标记都不用

#include<bits/stdc++.h>
using namespace std;
const int N = 30005;
int n, m, head[N], ecnt;
struct edge
{
	int to, nxt;
}edg[N << 1];
void add(int u, int v)
{
	edg[++ecnt].to = v;
	edg[ecnt].nxt = head[u];
	head[u] = ecnt;
}
int dfn[N];//时间戳 
int top[N];//这个点所在重链的顶端节点 
int w[N];//新建序列的值 
int val[N];//原来节点的值 
void dfs2(int u, int f)
{
	dfn[u] = ++tim;
	w[tim] = val[u];//把原来节点和序列中元素对应 
	if(son[f] == u) top[u] = top[f];//重儿子所在重链的顶端节点和他父亲所在重链的顶端节点一个 
	else top[u] = u;//自己作为重链的顶端节点 
	if(son[u]) dfs2(son[u], u);//优先dfs重链，保证区间连续 
	for(int i = head[u]; i; i = edg[i].nxt)
	{
		int v = edg[i].to;
		if(v != f && v != son[u]) dfs2(v, u);//dfs其他儿子 
	}
}
int sum[N << 2], maxn[N << 2];
void pushup(int cnt)
{
	sum[cnt] = sum[cnt << 1] + sum[cnt << 1 | 1];
	maxn[cnt] = max(maxn[cnt << 1], maxn[cnt << 1 | 1]);
}
void build(int cnt, int l, int r)
{
	if(l == r)
	{
		sum[cnt] = maxn[cnt] = w[l];
		return;
	}
	int mid = l + r >> 1;
	build(cnt << 1, l, mid);
	build(cnt << 1 | 1, mid + 1, r);
	pushup(cnt);
}
void update(int cnt, int l, int r, int x, int k)
{
	if(l == r)
	{
		sum[cnt] = maxn[cnt] = k;
		return;
	}
	int mid = l + r >> 1;
	if(x <= mid) update(cnt << 1, l, mid, x, k);
	else if(x > mid) update(cnt << 1 | 1, mid + 1, r, x, k);
	pushup(cnt);
}
int query1(int cnt, int l, int r, int nl, int nr)
{
	if(l >= nl && r <= nr) return sum[cnt];
	int ans = 0, mid = l + r >> 1;
	if(nl <= mid) ans += query1(cnt << 1, l, mid, nl, nr);
	if(nr > mid) ans += query1(cnt << 1 | 1, mid + 1, r, nl, nr);
	return ans;
}
int query2(int cnt, int l, int r, int nl, int nr)
{
	if(l >= nl && r <= nr) return maxn[cnt];
	int ans = -99999999, mid = l + r >> 1;
	if(nl <= mid) ans = max(ans, query2(cnt << 1, l, mid, nl, nr));
	if(nr > mid) ans = max(ans, query2(cnt << 1 | 1, mid + 1, r, nl, nr));
	return ans;
}
int querysum(int u, int v)
{
	int ans = 0;
	while(top[u] != top[v])//不在一条重链上 
	{
		if(dep[top[u]] < dep[top[v]]) swap(u, v);//找顶端节点深度较大的 
		ans += query1(1, 1, n, dfn[top[u]], dfn[u]);
		u = fa[top[u]];
	}//在同一条重链上 
	if(dfn[u] > dfn[v]) swap(u, v);
	ans += query1(1, 1, n, dfn[u], dfn[v]);
	return ans;
}
int querymax(int u, int v)
{
	int ans = -99999999;
	while(top[u] != top[v])
	{
		if(dep[top[u]] < dep[top[v]]) swap(u, v);
		ans = max(ans, query2(1, 1, n, dfn[top[u]], dfn[u]));
		u = fa[top[u]];
	}
	if(dfn[u] > dfn[v]) swap(u, v);
	ans = max(ans, query2(1, 1, n, dfn[u], dfn[v]));
	return ans;
}
int main()
{
	scanf("%d", &n);
	for(int i = 1; i < n; i ++)
	{
		int u, v;
		scanf("%d%d", &u, &v);
		add(u, v);add(v, u);
	}
	for(int i = 1; i <= n; i ++) scanf("%d", &val[i]);
	dfs1(1, 0);
	dfs2(1, 0);
	build(1, 1, n);
	scanf("%d", &m);
	for(int i = 1; i <= m; i ++)
	{
		int x, y;
		char opt[10];
		cin >> opt;
		scanf("%d%d", &x, &y);
		if(opt[1] == 'H') update(1, 1, n, dfn[x], y);
		if(opt[1] == 'M') printf("%d
", querymax(x, y));
		if(opt[1] == 'S') printf("%d
", querysum(x, y));
	}
}