Manacher
manacher是一种(O(n))求最长回文子串的算法,俗称马拉车(滑稽)
直接步入正题
首先可以知道的是:每一个回文串都有自己的对称中心,相应的也有自己的最大延伸长度(可以称之为“半径”)
我们设(rad[i])表示以(i)为中心的回文子串的半径,那么只需要知道所有的(rad[i])就可以求出最长回文子串了
从(1)到(n)枚举(i),求解(rad[i])
设当前已经求到了(rad[k]),设前(k-1)个数中(rad[i]+i)(即右端点)最大的数为(mid),令(r=mid+rad[mid])
那么可以证明一个点(i)关于(mid)的对称点是(2 imes mid-i)(两点距离公式)
opt1:如果(kleq r)
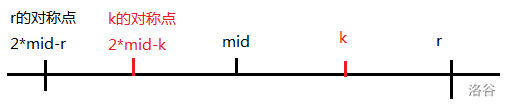
方便起见,令(j=2 imes mid-k)
1.若(j-rad[j]>mid-rad[mid]),即以(j)点为中心的最长回文子串的左端点在以(mid)为中心的最长回文子串的左端点右边,则(rad[i])可以直接由(rad[j])转移过来(因为(2 imes mid-r)~(mid)和(mid)~(r)是对称的,所以(k)的半径和(j)的半径是一样的),即(rad[i]=rad[j])
2.若(j-rad[j]leq mid-rad[mid]),则(rad[k])至少是(r-k)。接下来再暴力延伸,顺便更新(mid)和(r)
opt2:如果(k>r)
直接暴力延伸,顺便更新(mid)和(r)
可以发现每次暴力延伸的时候,暴力延伸多少,(r)也会变化多少,且(r)是递增的且不超过(n)的数
关于复杂度:
由于每一个字符最多只会被遍历一次,所以复杂度是(O(n))的
实现细节:
1.由于长度为偶数的回文串对称中心并不能实际找到,所以在两个字符之间插入#。这样不会影响答案,并且可以解决这个问题
2.对于不同情况的相似之处可以合并到一起来降低码量,如op1.1的直接转移和opt1.2的转移等
3.不要忘了更新(mid)和(r)
4.注意下标
代码:
#include<bits/stdc++.h>
using namespace std;
char cString[22000005];
int iRad[22000005];
int iLen,iAns;
void read()
{
char c = getchar();
cString[0] = '|', cString[++iLen] = '#';
while(c < 'a' || c > 'z') c = getchar();
while(c >= 'a'&& c <= 'z') cString[++iLen] = c, cString[++iLen] = '#', c = getchar();
}
int main()
{
read();//读入
for(int i = 1, mid = 0, r = 0; i <= iLen; i++)
{
if(i <= r) iRad[i] = min(iRad[mid * 2 - i], r - i + 1);//opt1
while(cString[i - iRad[i]] == cString[i + iRad[i]]) ++iRad[i];//opt1.2,opt2 尝试暴力延伸
if(i + iRad[i] > r) r = i + iRad[i] - 1, mid = i;//更新mid和r
if(iRad[i] > iAns) iAns = iRad[i];//更新答案
}
printf("%d", iAns-1);
}