浅谈网络最大流

什么是网络最大流？

通俗的来讲，就是给你一个图，有水流从源点S流经很多路线，问你最终能到达汇点S的水流最大是多少。

比如这张图

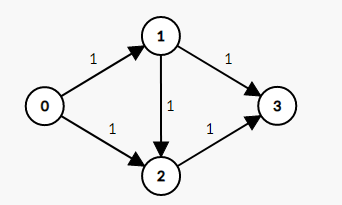
从原点0到汇点3的最大流就是2，路线是0→1→3和0→2→3

那么对于这个网络有几条显然的性质：

1.除了源点和汇点，流进每个点的流量=流出每个点的流量

2.每条边的实际流量不能大于它的最大容量

EK（Edmond—Karp）增广路算法

什么是增广路？

增广路是指从S到T的一条路，流过这条路，使得当前的流量可以增加。

那你求最大流的过程不就是不断寻找能够使流量增加的增广路的问题吗？

显然当没有增广路时就出来答案了。

那怎么寻找增广路？

EK算法就是通过bfs来找增广路。

从s开始不断向外广搜，通过权值大于0的边（因为后面会减边权值，所以可能存在边权为0的边），直到找到t为止，然后找到该路径上边权最小的边，记为mi，然后最大流加mi，然后把该路径上的每一条边的边权减去mi，直到找不到一条增广路（从s到t的一条路径）为止。

上面一小段是洛谷日报的话

举个栗子：我们现在有这样一张图

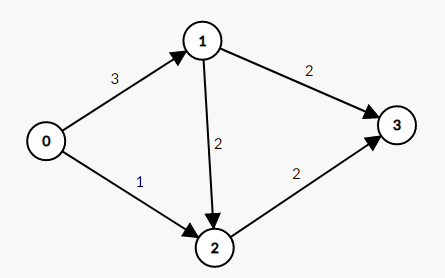
假设我们从0开始bfs后，走到1，从1开始bfs，走到3。这就出现了一条增广路。我们把走过的边加红处理

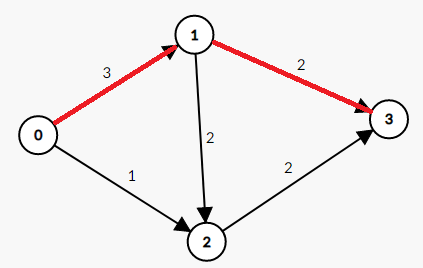
在这一条增广路上最小的边为1->3=2，那么我们把加红的边的权值都减去2

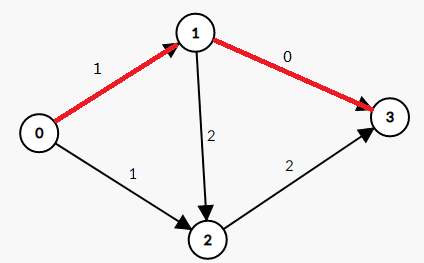
同理，再找到一条增广路0->2->3，这条路上最小的权值是1，那么我们把这条路径上的边的权值都减去1

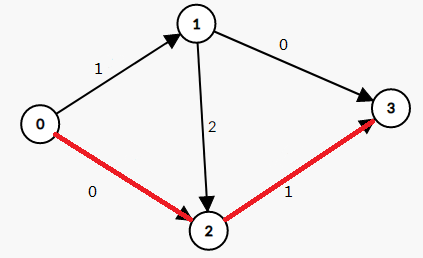
然后又有0->1->2->3，相同的处理

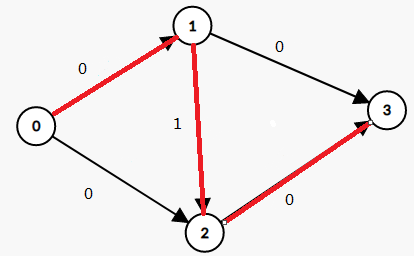
那么最后的答案就是4

看到这里可能有人要问了。如果我在bfs 1->3这条路径之前先bfs了1->2，那最后的答案不就是不对了吗？

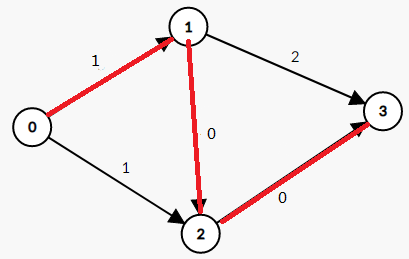
是的。正因为bfs会考虑所有的情况，自然也会有不优的解。为了防止这种情况的发生，我们设置一个神奇的东西——反向边

为什么要建反向边？一会儿你就知道了

如图，刚开始反向边的权值都是0

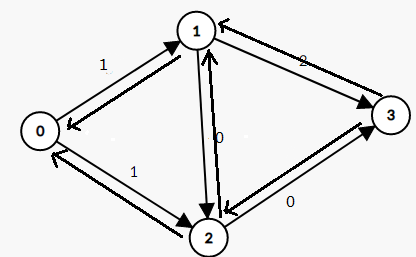
在你进行对原有的边减去增广路上最小边的操作时，把反向边的权值加上这个值

这会产生什么影响？

发现在对一个点bfs的时候，也会走反向边。

对！反向边的作用就是使程序有反悔的机会。

时间复杂度O(nm²)，实际运用中能够处理10³~10⁴的网络

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+6,M=2e5+6,inf=1e9+7;
int n,m,s,t,ans,now[N],pre[N];
bitset<N> v;

struct edge 
{
    int to,dis,nxt;
}edg[M];
int head[N],cnt=1;

inline void add(int u,int v,int w)
{
    edg[++cnt].dis=w;
    edg[cnt].to=v;
    edg[cnt].nxt=head[u];
    head[u]=cnt;
}

inline bool bfs()//寻找增广路 
{
    v.reset();
    queue<int> q;
    q.push(s);
    v[s]=1;
    now[s]=inf;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=edg[i].nxt)
        {
            int y=edg[i].to,z=edg[i].dis;
            if(v[y]||!z) continue ;
            now[y]=min(now[x],z);
            pre[y]=i;
            if(y==t) return 1;
            q.push(y);
            v[y]=1;
        }
    }
    return 0;
}

inline void upd()//更新 
{
    ans+=now[t];
    int x=t;
    while(x!=s)
    {
        int i=pre[x];
        edg[i].dis-=now[t];
        edg[i^1].dis+=now[t];
        x=edg[i^1].to;
    }
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
        add(v,u,0);//反向边 
    }
    while(bfs()) upd();
    cout<<ans;
}

Dinic算法

残余网络：网络中所有节点以及剩余容量大于0的边组成残余网络

EK算法慢的原因是它每次有可能遍历整个残余网络但是只找出一条增广路

dinic算法就是每次寻找多条增广路的算法

我们引入一个分层图的概念

按照节点到源点的距离（或者说是最少经过的边数）分层

先用bfs对残余网络分层

然后用dfs从当前一层向后一层反复寻找增广路

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+6,M=2e5+6,inf=1e9;
int n,m,s,t,ans,d[N];

struct edge
{
    int to,dis,nxt;
}edg[M];
int head[N],cnt=1;

inline void add(int u,int v,int w)
{
    edg[++cnt].dis=w;
    edg[cnt].to=v;
    edg[cnt].nxt=head[u];
    head[u]=cnt;
}

inline bool bfs()//分层 
{
    memset(d,0,sizeof(d));
    queue<int> q;
    q.push(s);
    d[s]=1;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for(int i=head[x];i;i=edg[i].nxt)
        {
            int y=edg[i].to,z=edg[i].dis;
            if(d[y]||!z) continue;
            q.push(y);
            d[y]=d[x]+1;
            if(y==t) return 1;
        }
    }
    return 0;
}

int dfs(int u,int w)//当前的点,流入当前点的流量 
{
    if(u==t) return w;
    int sum=0;
    for(int i=head[u];i;i=edg[i].nxt)
    {
        int v=edg[i].to;
        if(edg[i].dis<=0||d[v]!=d[u]+1) continue;//流向下一层 
        int l=dfs(v,min(w-sum,edg[i].dis));//受最大流量限制 
        edg[i].dis-=l;//更新 
        edg[i^1].dis+=l;
        sum+=l;//当前已经使用的流量 
        if(sum=w) break;//一个剪枝 
    }
    if(sum>=w) d[u]=-1;
    return sum;
}

int main()
{
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
        add(v,u,0);
    }
    int a;
    while(bfs())
    {
        while(a=dfs(s,inf)) ans+=a;
    }
    printf("%d
",ans);
}