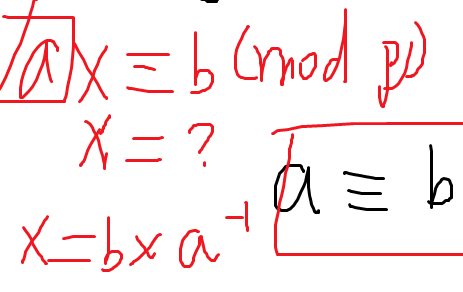内容提要
搜索
拓展欧几里得
逆元
先是搜索
A*
有几个数组
g 当前点到根节点的深度
h 当前点到终点理想的最优情况需要走几步
f f=g+h
A*就是把所有的f从小到大排序
启发式搜索相较于其他的搜索的优势在于引入了一个启发式函数f(x) = g(x) +h(x)
g*(x) : 从 S 到 x 的理论最近距离
g(x) : 对 S 到 x 对于 g*(x) 的估计
f*(x) : 从 x 到 T 的理论最近距离,F*(x)=g*(x)+h*(x)
f(x) : 从 x 到 T 对于 f*(x) 的估计,F(x)=g(x)+h(x)
可以理解为:带*的是开挂的,不带*的是真实的
当满足 f(x) <= f*(x) 时,总能找到最优解
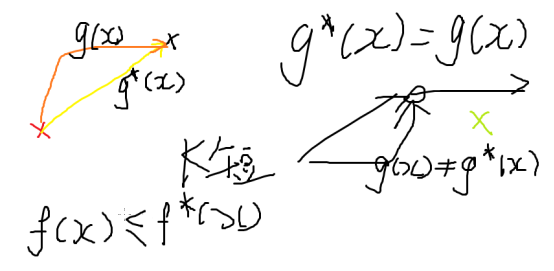
和 BFS 几乎一样,只是每次都弹出当前局面中f(x)最小的那个局面进行扩展
——故需要维护一个优先队列(小根堆)
——使用系统的priority_queue<>即可
当 f(x) = g(x) + h(x) 中 h(x) = 0 即失去了启发式函数,则变为Breath First Search
当 f(x) = g(x) + h(x) 中 g(x) = 0 则变为 Best First Search
当第一次到终点的时候就输出g(x)就可以了
例题:八数码
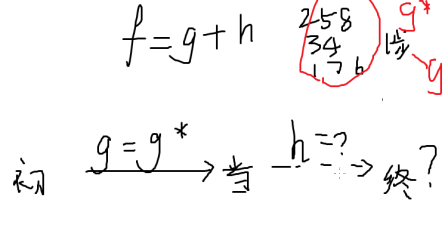
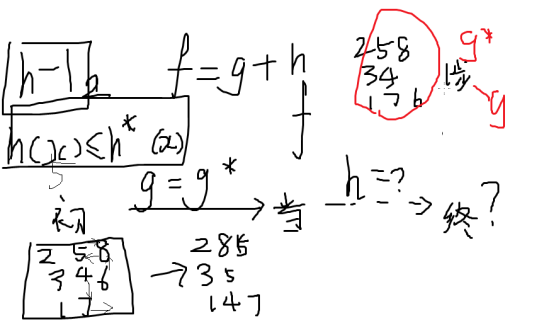
如何告诉计算机某种情况已经到达过呢:
如何做到将一个 1~n 的排列与一个整数做一一对应?
或者更直白的:
如何求出字典序第 k 的排列?
如何求出一个排列在字典序中排第几?

这样数组只需要开9!=36880
#include <cstdio> #include <cstring> #include <cstdlib> #include <queue> const int sizeofpoint=1024; const int sizeofedge=262144; int N, M; int S, T, K; int d[sizeofpoint], t[sizeofpoint]; struct node { int u; int g; inline node(int _u, int _g):u(_u), g(_g) {} }; inline bool operator > (const node & , const node & ); struct edge { int point; int dist; edge * next; }; inline edge * newedge(int, int, edge * ); inline void link(int, int, int); edge memory[sizeofedge], * port=memory; edge * e[sizeofpoint], * f[sizeofpoint]; std::priority_queue<node, std::vector<node>, std::greater<node> > h; inline int getint(); inline void dijkstra(int); inline int Astar(); int main() { N=getint(), M=getint(); for (int i=1;i<=M;i++) { int u=getint(), v=getint(), d=getint(); link(u, v, d); } S=getint(), T=getint(), K=getint(); dijkstra(T); if (d[S]==-1) { puts("-1"); return 0; } K+=S==T; printf("%d ", Astar()); return 0; } inline bool operator > (const node & u, const node & v) { return (u.g+d[u.u])>(v.g+d[v.u]); } inline edge * newedge(int point, int dist, edge * next) { edge * ret=port++; ret->point=point, ret->dist=dist, ret->next=next; return ret; } inline void link(int u, int v, int d) { e[v]=newedge(u, d, e[v]); f[u]=newedge(v, d, f[u]); } inline int getint() { register int num=0; register char ch; do ch=getchar(); while (ch<'0' || ch>'9'); do num=num*10+ch-'0', ch=getchar(); while (ch>='0' && ch<='9'); return num; } inline void dijkstra(int S) { static int q[sizeofedge]; static bool b[sizeofpoint]; int l=0, r=0; memset(d, 0xFF, sizeof(d)), d[S]=0; for (q[r++]=S, b[S]=true;l<r;l++) { int u=q[l]; b[u]=false; for (edge * i=e[u];i;i=i->next) if (d[i->point]==-1 || d[u]+i->dist<d[i->point]) { d[i->point]=d[u]+i->dist; if (!b[i->point]) { b[i->point]=true; q[r++]=i->point; } } } } inline int Astar() { h.push(node(S, 0)); while (!h.empty()) { node p=h.top(); h.pop(); ++t[p.u]; if (p.u==T && t[T]==K) return p.g; if (t[p.u]>K) continue; for (edge * i=f[p.u];i;i=i->next) h.push(node(i->point, p.g+i->dist)); } return -1; }
IDA*
g:从根节点往下几步
h:步数
g+h>d return
双向A*?双向IDA*?
h(x)>h*(x)?
事实上h(x)与h*(x)的关系隐形决定了A*的运行速度与准确度
h(x)越接近h*(x)跑得越快
拓展欧几里得
裴蜀定理:(x, y) = d ===> 存在无限多组整数 a,b:ax + by = d
证明:计算机竞赛不需要证明
扩展欧几里得算法可以帮助我们计算出 (x, y) = d 时一组 a,b:

什么?你问为什么?这么短的代码你背下来不就好了嘛?
扩展欧几里得算法有什么用呢?——计算逆元
逆元的定义:如果 x 对 p 有一个逆元 y,则 x * y == 1 (mod p)
x 对一个数 p 有逆元当且仅当 (x, p) = 1
意义:在取模意义下做除法
由裴蜀定理:存在 a, b 满足:ax + bp = 1
嗯……,等等,岂不是 ax == 1 (mod p)

计算组合数模p
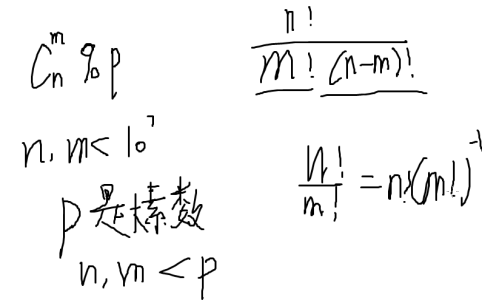
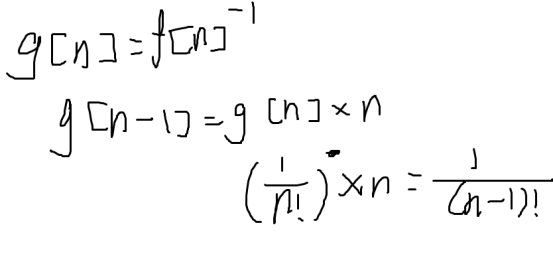

中国剩余定理
问题、求余方程组 x = ai (mod pi)
不多说,背代码:
令 P = p1 * p2 * ... * pn
令 Pi = P / pi
令 Qi = Pi 对 pi 的逆元
则 x = sigma(ai * Pi * Qi)