一道大模拟
思路:
首先是打表找规律时间
仔细思考(暴力手算)后推出这么一个数组:
//宽的增加量 int dm[4]={0,0,4,2};//1竖着摞,2横着摞,3前后摞 //长的增加量 int dn[4]={0,3,0,2};//1竖着摞,2横着摞,3前后摞
这是什么意思呢?在初始的情况下,一个正方体的长是7个字符(对应了二维图的宽,就是y),高是6个字符(对应了二维图的长,就是x)
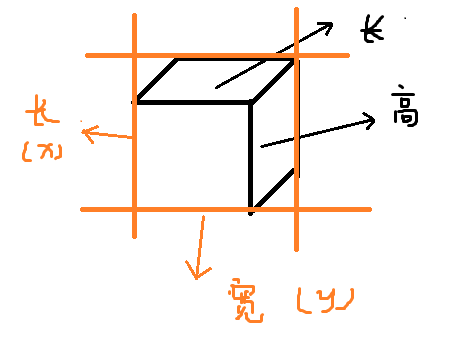 如图,橙色表示二维图的参数,黑色表示三维正方体的参数
如图,橙色表示二维图的参数,黑色表示三维正方体的参数
我们用1表示竖着摞,2表示横着摞,3表示前后摞
我们发现
- 每竖着摞一个正方体,二维图的宽是不会变的,但是长会在6的基础上+3
- 每横着摞一个正方体,二维图的宽在7的基础上增加4,长不变
- 每前后摞一个正方体,二维图的长和宽都在原来的基础上增加2
我们既然要输出最后的图,显然要先求出他的长和宽
宽是比较好求的,因为宽只与横着摞和前后摞有关,而这两个方式都可以直接又输入的n和m得出。设mm为输出图的宽,则:
mm=7+(n-1)*dm[3]+(m-1)*dm[2];
而长就不一样了,长不但与前后摞有关,还与上下摞有关,因为我没有ybr神仙那么强,所以我决定枚举。
for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { nn=max(nn,atlas[i][j]*dn[1]+dn[3]*(n-i+1)+1); //枚举每一个点的长,取最大值 } }
于是我们就求出了长和宽,接下来考虑处理图。可以用一个点来代表整张图,这里我选择左下角的点,可以根据当前的位置(给的矩阵的某个位置)推出左下角的点,然后进行覆盖就好了。由于是按照从后向前,从左到右的顺序进行处理的,所以后来的会把先来的覆盖上,就处理了透视的问题
完整代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> #include<cmath> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,m; char s1[6][8]= { "..+---+", "./ /|", "+---+ |", "| | +", "| |/.", "+---+.." }; //宽的增加量 int dm[4]={0,0,4,2};//1竖着摞,2横着摞,3前后摞 //长的增加量 int dn[4]={0,3,0,2};//1竖着摞,2横着摞,3前后摞 char s[1000][1000]; int atlas[51][51]; int mm,nn; inline void zhetizhenduliu(int i,int j,int x,int y) { int a,b; while(atlas[i][j]--) { for(a=0;a<6;a++) for(b=0;b<7;b++) if(s1[6-a-1][b]!='.') s[x-a][y+b]=s1[6-a-1][b]; x-=3; } } int main() { //freopen("drawing.in","r",stdin); //freopen("drawing.out","w",stdout); n=read(),m=read(); for(int i=1;i<=1000;i++) { for(int j=1;j<=1000;j++) { s[i][j]='.'; } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { atlas[i][j]=read(); } } if(m==1&&n==1&&atlas[1][1]==1) { printf("..+---+ ./ /| +---+ | | | + | |/. +---+.. "); return 0; } mm=7+(n-1)*dm[3]+(m-1)*dm[2];//求出输出的宽 for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { nn=max(nn,atlas[i][j]*dn[1]+dn[3]*(n-i+1)+1); //枚举每一个点的长,取最大值 } } for(int i=1;i<=n;i++) { for(int j=1,x,y;j<=m;j++) { x=nn-dn[3]*(n-i);//考虑倒着搞,i前面的会产生2*(n-i)的影响 y=dm[3]*(n-i)+dm[2]*(j-1)+1; zhetizhenduliu(i,j,x,y); } } for(int i=1;i<=nn;i++) { for(int j=1;j<=mm;j++) { printf("%c",s[i][j]); } puts(""); } }
PS:由于我太蒟了,考试的时候想到了做法但是覆盖的地方写炸,所以后来借鉴了题解(竟然和我思路差不多)