前置知识:如果不了解的话建议先去了解一下
KMP:传送门
Trie字典树:传送门
咳咳,那么如果你到了这里,说明你已经会了KMP和Trie了(至少会了板子)
我们发现KMP是单模式串匹配单主串的算法
Trie是查找字符串的算法
那么如果我们要处理多模式串匹配单主串应该怎么办呢?
这就要用到AC自动机了
可以简单的理解为将KMP放在Trie树上
最常见的例子就是给出n个单词Ti和一段文本S,问你有多少个单词在文本中出现
构建AC自动机的主要步骤:
1.将所有的模式串构建成一棵Trie树
2.对Trie上的所有节点构造前缀指针(或者失败指针,失配指针)
3.利用前缀指针对主串进行匹配
如果你对KMP了解的话,应该知道里面的next数组(或者fail数组,p数组)是干什么用的
我们用两个指针i和j分别表示A[i-j+1......i]和B[1......j]完全相等,也就是说i是不断增加的,并且随着i的增加,j也相应的变化,并且j满足以A[j]结尾的长度为j的字符串正好匹配B串的前j个字符,当A[i+1]和B[j+1]不相等的时候,我们不是重新开始匹配,而是调整j的位置,而next数组就是记录了这个位置
同样,AC自动机的前缀指针(失配指针)也是起了这个作用。就是当你匹配失败的,时候应该跳到指针指向的地方继续匹配
接下来我们一步一步的讲解
1.建立trie树
- 这个没什么好说的,就是普通的字典树建树
2.建立nxt数组(也就是前缀指针)
nxt[u]表示当匹配到u节点而u的转移边都无法匹配的时候,满足最长前后缀关系的新的u节点,也就是所有满足T'[1...k]=T[j-k+1]的k(k<j)的最大值所对应的节点编号
显然nxt[u]的节点的深度是小于u节点的,因此我们可以按照节点的深度大小,也就是bfs的顺序构建nxt数组。
我们设v,u分别表示字符串T'[1...i]和T[1...j],其中v是u的后缀并且nxt[u]=v。枚举u的转移边指向的转移节点x,现在我们要求出nxt[x]。
- 若T'[i+1]=T[j+1],也就是下一位仍然匹配,那么设v的相同字符转移边为y,令nxt[x]=y
- 否则T'[i+1]与T[j+1]失配,我们领v=nxt[v],即跳到字符串v的后缀nxt[v]处,按照以上的过程继续匹配。
- 如果跳到了空节点,则无法匹配,nxt[x]=0
举个例子:
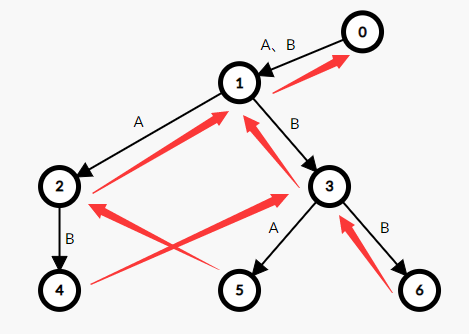
首先定义虚拟节点0,将0号节点的所有连出的边都指向1号节点

1号节点的前缀指针指向0号节点
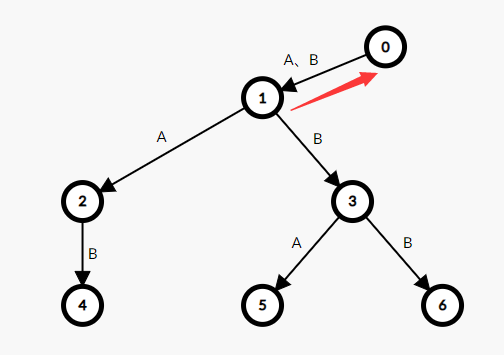
2号节点:父亲是1号节点,连接字符为A,查找父亲的前缀指针0号节点,看看是否有通过A连接的儿子
有,于是2号节点的前缀指针指向1号节点
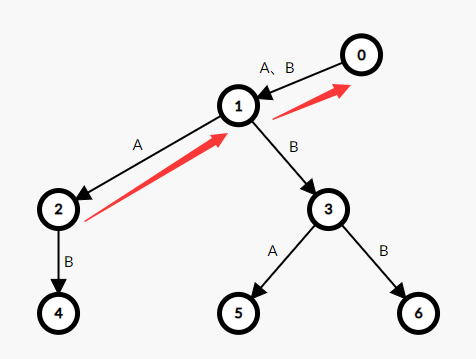
3号节点:父亲是1号节点,连接字符为B,查找父亲的前缀指针0号节点,看看是否有通过B连接的儿子
有,于是3号节点的前缀指针指向1号节点
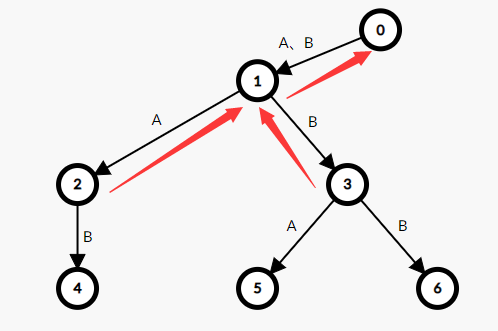
4号节点:父亲是2号节点,连接字符为B,查找父亲的前缀指针1号节点,看看是否有通过B连接的儿子
有,于是4号节点的前缀指针指向3号节点
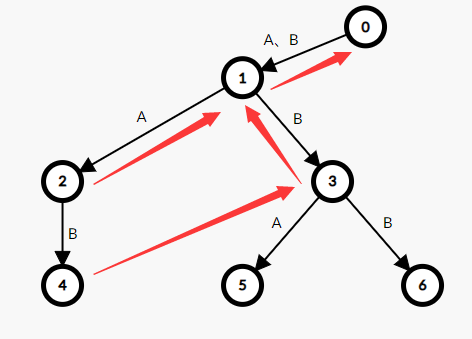
5号节点:父亲是3号节点,连接字符为A,查找父亲的前缀指针1号节点,看看是否有通过A连接的儿子
有,于是5号节点的前缀指针指向2号节点

6号节点:父亲是3号节点,连接字符为B,查找父亲的前缀指针1号节点,看看是否有通过B连接的儿子
有,于是6号节点的前缀指针指向3号节点
代码:
queue<int> q; inline void get_nxt() { rep(i,0,25) ch[0][i]=1; //初始化0节点的所有转移边都指向1 nxt[1]=0;//初始化1的前缀指针指向0 q.push(1);//先让1入队 while(!q.empty()) { int now=q.front();//取出队首元素 q.pop(); rep(i,0,25) { int u=ch[now][i]; if(!u) //如果节点now没有以i为转移边的节点 ch[now][i]=ch[nxt[now]][i]; //就继续向前寻找now的前缀指针指向的节点以i为转移边的节点 else //如果节点now有以i为转移边的节点 { q.push(u);//先入队 int v=nxt[now]; nxt[u]=ch[v][i]; //节点u的前缀指针为u的前缀指针通过转移边i连接的儿子 } } } }
3.主串和模式串的匹配
首先,指针指向根节点
依次读入单词,检查是否存在这个子节点
然后指针跳转到子节点
如果不存在
直接跳转到失配指针即可
代码:
inline void find(char s[]) { int now=1,len=strlen(s),c,k; rep(i,0,len-1)//在字典树上查找该单词 { c=s[i]-'a'; k=ch[now][c]; while(k>1) { if(bo[k]==-1) break; //注意这里要break掉已经查找过的单词,否则会tle ans+=bo[k];//这里是为了加上重复单词 bo[k]=-1; k=nxt[k];//转移 } now=ch[now][c]; } return ; }
最后组合一下就是AC代码了:
#include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<time.h> #include<queue> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head const int N=1e6+5; int n,t,ans,cnt; int ch[N][26],nxt[N],bo[N],que[N]; inline void build(char s[]) { int now=1,len=strlen(s); rep(i,0,len-1) { int c=s[i]-'a'; if(!ch[now][c]) { ch[now][c]=++cnt; }//如果还没有这个节点,就新创建一个节点 now=ch[now][c];//当前节点转移过去 } bo[now]++;//给以节点now为终止节点的打上标记 return; } queue<int> q; inline void get_nxt() { rep(i,0,25) ch[0][i]=1; //初始化0节点的所有转移边都指向1 nxt[1]=0;//初始化1的前缀指针指向0 q.push(1);//先让1入队 while(!q.empty()) { int now=q.front();//取出队首元素 q.pop(); rep(i,0,25) { int u=ch[now][i]; if(!u) //如果节点now没有以i为转移边的节点 ch[now][i]=ch[nxt[now]][i]; //就继续向前寻找now的前缀指针指向的节点以i为转移边的节点 else //如果节点now有以i为转移边的节点 { q.push(u);//先入队 int v=nxt[now]; nxt[u]=ch[v][i]; //节点u的前缀指针为u的前缀指针通过转移边i连接的儿子 } } } } inline void find(char s[]) { int now=1,len=strlen(s),c,k; rep(i,0,len-1)//在字典树上查找该单词 { c=s[i]-'a'; k=ch[now][c]; while(k>1) { if(bo[k]==-1) break; //注意这里要break掉已经查找过的单词,否则会tle ans+=bo[k];//这里是为了加上重复单词 bo[k]=-1; k=nxt[k];//转移 } now=ch[now][c]; } return ; } int main() { char s[N<<1]; ans=0,cnt=1; rep(i,0,25) { ch[0][i]=1,ch[1][i]=0; } n=read(); rep(i,1,n) { scanf("%s",s); build(s); } get_nxt(); scanf("%s",s); find(s); printf("%d ",ans); }
queue<int> q;inline void get_nxt(){ rep(i,0,25) ch[0][i]=1; //初始化0节点的所有转移边都指向1 nxt[1]=0;//初始化1的前缀指针指向0 q.push(1);//先让1入队 while(!q.empty()) { int now=q.front();//取出队首元素 q.pop(); rep(i,0,25) { int u=ch[now][i]; if(!u) //如果节点now没有以i为转移边的节点 ch[now][i]=ch[nxt[now]][i]; //就继续向前寻找now的前缀指针指向的节点以i为转移边的节点 else //如果节点now有以i为转移边的节点 { q.push(u);//先入队 int v=nxt[now]; nxt[u]=ch[v][i];//节点u的前缀指针为u的前缀指针通过转移边i连接的儿子 } } }}