一.什么是线段树
线段树之所以称为“树”，是因为其具有树的结构特性。线段树由于本身是专门用来处理区间问题的
线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
同一层的节点所代表的区间，相互不会重叠
同一层节点所代表的区间，加起来是个连续的区间
对于每一个非叶结点所表示的结点[a,b]，其左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b](除法去尾取整）
叶子节点表示的区间长度为1.
同一层节点所代表的区间，加起来是个连续的区间
对于每一个非叶结点所表示的结点[a,b]，其左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b](除法去尾取整）
叶子节点表示的区间长度为1.
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。
举几个线段树的例子
①n=10
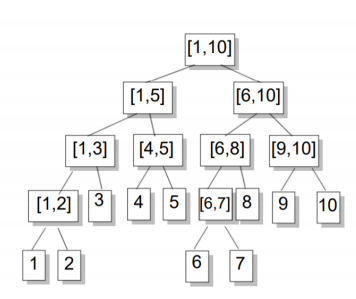
②n=9
二.线段树的构造与实现
1.建树与维护
根据线段树的性质，我们可以得到一个节点的左儿子和右儿子的表示方法（上面有提QwQ）
inline ll ls(ll x)//左儿子 { return x<<1;//相当于x*x } inline ll rs(ll x)//右儿子 { return (x<<1)|1;//相当于x*2+1 }
于是就有了维护的代码：
inline void push_up_sum(ll p)//向上维护区间和 { ans[p]=ans[ls(p)]+ans[rs(p)]; } inline void push_up_min(ll p)//向上维护区间最小值 { ans[p]=min(ans[ls(p)],ans[rs(p)]); } inline void push_up_max(ll p)//向上维护区间最大值 { ans[p]=max(ans[ls(p)],ans[rs(p)]); }
需要注意的是，这里是从下往上维护父子节点的逻辑关系，因为当你一个子节点改变了之后，它所有的父亲节点都需要改变。所以开始递归之后必然是先去整合子节点的信息，再向它们的祖先反馈整合之后的信息。
所以对于建树，由于二叉树的结构特点，我们可以选择递归建树，并且在递归的过程中要注意维护父子关系
void build(ll p,ll l,ll r)//p 根节点,l 区间左端点,r 区间右端点 { tag[p]=0;//建树时顺便把懒惰标记清零(这个后面会提到) if(l==r)//如果左右端点相等,就说明已经到达了叶子结点 { ans[p]=a[l]; return ; } ll mid=(l+r)>>1;//左右子树分别递归建树 build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p);//记得维护父子关系 }
我们已经有了一棵线段树，但是现在并不能对它进行什么操作，它目前还并没有什么卵用
2.区间修改
假如我们要修改一个区间[l,r]内的值，我们发现由于二叉树的结构特点，l和r很可能不在同一个节点上，这时候怎么办？
区间拆分了解一下
区间拆分是线段树的核心操作,我们可以将一个区间[a, b]拆分成若干个节点,使得这些节点代表的区间加起来是[a, b],并且相互之间不重叠.
所有我们找到的这些节点就是”终止节点”.
区间拆分的步骤
从根节点[1, n]开始，考虑当前节点是[L, R].
如果[L, R]在[a, b]之内,那么它就是一个终止节点.
否则,分别考虑[L, Mid],[Mid + 1, R]与[a, b]是否有交,递归两边继续找终止节点
举个栗子：
比如我们要从[1,10]中拆分出[2,8]这个区间
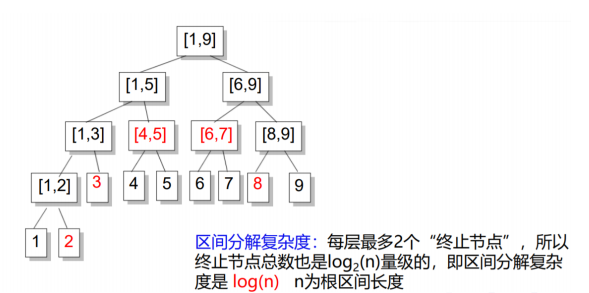
还是挺直观的吧QwQ
这其实是一种分块的思想
分块的思想是通过将整个序列分为有穷个小块，对于要查询的一段区间，总是可以整合成k个所分块与m个单个元素的信息的并
所以我们应该充分利用区间拆分的性质，思考在终止节点要存什么信息，如何快速维护这些信息，不要每次一变就到最底层
那么对于区间操作，我们引入一个东西——懒标记(lazy tag)。那这个东西“lazy”在什么地方呢？
我们发现原本的区间修改需要通过改变最下的叶子结点，然后不断向上递归来修改祖先节点直至到达根节点，时间复杂度最多可以到O(n logn)的级别。
但是当我们用了懒标记后，时间复杂度就降低到了O(log n)的级别甚至更低
懒标记怎么用？
如果整个区间都被操作，就把懒标记记录在公共祖先节点上，如果只修改了一部分，就记录在这部分的公共祖先上，如果只修改了自己的话，就只改变自己
然后，如果我们采用这种方式优化的话，我们需要在每一次区间查询修改时pushdown一次，以免重复冲突
那么怎么传导push down呢？
开始回溯是执行push up，因为是向上传导信息；如果我们想要他向下更新，就调整顺序，在向下递归的时候push down
代码：
inline void f(ll p,ll l,ll r,ll k) { tag[p]=tag[p]+k; ans[p]=ans[p]+k*(r-l+1); //由于是这个区间统一改变，所以ans数组要加元素个数 } //f函数的唯一目的，就是记录当前节点所代表的区间 inline void push_down(ll p,ll l,ll r) { ll mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]=0; //不断向下递归更新子节点 } inline void update(ll nl,ll nr,ll l,ll r,ll p,ll k) { //nl,nr为要修改的区间 //l,r,p为当前节点所存储的区间以及节点的编号 //k为要增加的值 if(nl<=l&&r<=nr) { ans[p]+=k*(r-l+1); tag[p]+=k; return; } push_down(p,l,r); //回溯之前（也可以说是下一次递归之前，因为没有递归就没有回溯） //由于是在回溯之前不断向下传递，所以自然每个节点都可以更新到 ll mid=(l+r)>>1; if(nl<=mid) update(nl,nr,l,mid,ls(p),k); if(nr>mid) update(nl,nr,mid+1,r,rs(p),k); push_up(p); //回溯之后 }
对于复杂度而言，由于完全二叉树的深度不超过logn，那么单点修改显然是O(logn)的，而区间修改的话，由于我们是分了log n个区间，每次查询是O(1)的复杂度，所以复杂度是O(log n)的
3.区间查询
这里还是用到了分块的思想，对于要查询的区间做区间分解，然后递归求答案就好了
ll find(ll qx,ll qy,ll l,ll r,ll p) { //qx 区间左端点 qy区间右端点 //l当前左端点 r当前右端点 //p当前区间的编号 ll res=0; if(qx<=l&&r<=qy) return ans[p]; ll mid=(l+r)>>1; push_down(p,l,r); if(qx<=mid) res+=find(qx,qy,l,mid,ls(p)); if(qy>mid) res+=find(qx,qy,mid+1,r,rs(p)); return res; }
三.标程
#include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<time.h> #include<queue> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head const int MAXN=1000001; ll a[MAXN],ans[MAXN<<2],tag[MAXN<<2]; ll m,n; inline ll ls(ll x) { return x<<1; } inline ll rs(ll x) { return (x<<1)+1; } inline void push_up(ll p) { ans[p]=ans[ls(p)]+ans[rs(p)]; } inline void f(ll p,ll l,ll r,ll k) { tag[p]=tag[p]+k; ans[p]=ans[p]+k*(r-l+1); } inline void push_down(ll p,ll l,ll r) { ll mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]=0; } void build(ll p,ll l,ll r) { tag[p]=0; if(l==r) { ans[p]=a[l]; return ; } ll mid=(l+r)>>1; build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p); } inline void update(ll nl,ll nr,ll l,ll r,ll p,ll k) { if(nl<=l&&r<=nr) { ans[p]+=k*(r-l+1); tag[p]+=k; return; } push_down(p,l,r); ll mid=(l+r)>>1; if(nl<=mid) update(nl,nr,l,mid,ls(p),k); if(nr>mid) update(nl,nr,mid+1,r,rs(p),k); push_up(p); } ll find(ll qx,ll qy,ll l,ll r,ll p) { ll res=0; if(qx<=l&&r<=qy) return ans[p]; ll mid=(l+r)>>1; push_down(p,l,r); if(qx<=mid) res+=find(qx,qy,l,mid,ls(p)); if(qy>mid) res+=find(qx,qy,mid+1,r,rs(p)); return res; } int main() { n=read(),m=read(); rep(i,1,n) a[i]=read(); build(1,1,n); while(m--) { ll a1=read(); if(a1==1) { ll b=read(),c=read(),d=read(); update(b,c,1,n,1,d); } if(a1==2) { ll b=read(),c=read(); printf("%lld ",find(b,c,1,n,1)); } } return 0; }
特别鸣谢：_皎月半洒花 大佬题解
water_lift:
#include<bits/stdc++.h> using namespace std; typedef long long ll; const ll N=100001; ll sum[N<<2],lazy[N<<2]; ll a[N]; void build(ll cnt,ll l,ll r) { if(l==r) { sum[cnt]=a[l]; return; } else { ll mid=(l+r)>>1; build(cnt<<1,l,mid); build((cnt<<1)|1,mid+1,r); sum[cnt]=sum[cnt<<1]+sum[(cnt<<1)+1]; } } inline bool cover(ll nl,ll nr,ll l,ll r) { return l<=nl&&r>=nr; } inline bool intersection(ll nl,ll nr,ll l,ll r) { return l<=nr&&r>=nl; } void pushdown(ll cnt,ll l,ll r) { ll mid=(l+r)>>1; lazy[cnt<<1]+=lazy[cnt]; lazy[(cnt<<1)+1]+=lazy[cnt]; sum[cnt<<1]+=lazy[cnt]*(mid-l+1); sum[(cnt<<1)+1]+=lazy[cnt]*(r-mid); lazy[cnt]=0; } void add(ll cnt,ll nl,ll nr,ll l,ll r,ll a) { if(cover(nl,nr,l,r)) { sum[cnt]+=(nr-nl+1)*a; lazy[cnt]+=a; return ; } pushdown(cnt,nl,nr); ll mid=(nl+nr)>>1; if(intersection(nl,mid,l,r)) add(cnt<<1,nl,mid,l,r,a); if(intersection(mid+1,nr,l,r)) add(cnt<<1|1,mid+1,nr,l,r,a); sum[cnt]=sum[cnt<<1]+sum[cnt<<1|1]; } ll query(ll cnt,ll nl,ll nr,ll l,ll r) { if(cover(nl,nr,l,r)) { return sum[cnt]; } pushdown(cnt,nl,nr); ll mid=(nl+nr)>>1; ll ans=0; if(intersection(nl,mid,l,r)) ans+=query(cnt*2,nl,mid,l,r); if(intersection(mid+1,nr,l,r)) ans+=query(cnt*2+1,mid+1,nr,l,r); return ans; } ll n,m; int main() { cin>>n>>m; for(ll i=1;i<=n;i++) cin>>a[i]; build(1,1,n); while(m--) { ll k; scanf("%lld",&k); if(k==1) { ll l,r,t; scanf("%lld%lld%lld",&l,&r,&t); add(1,1,n,l,r,t); } else if(k==2) { ll l,r; scanf("%lld%lld",&l,&r); printf("%lld ",query(1,1,n,l,r)); } } }