唉,上午就碰到一个开不了机的电脑,白白浪费了半个小时,真的难受QwQ
POINT1 枚举
枚举也称作穷举,指的是从问题所有可能的解的集合中一一枚举各元素。
用题目中给定的检验条件判定哪些是无用的,哪些是有用的。能使命题成立的即为其解。
例一
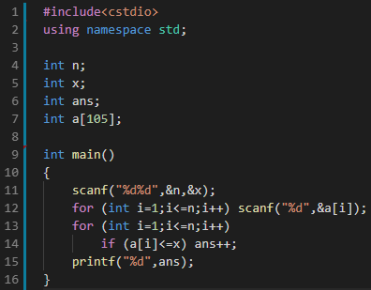
一棵苹果树上有n个苹果,每个苹果长在高度为Ai的地方。
小明的身高为x他想知道他最多能摘到多少苹果
数据范围: 1 ≤ n, Ai, x ≤ 100
题解
问题相当于询问有多少i满足Ai <= x,考虑用for循环枚举每一个苹果是否能被摘到即可
例二
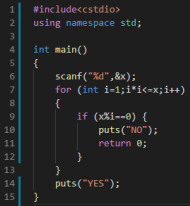
判断一个数X是否是素数
1 ≤ X ≤ 10
考虑定义,若X为合数,则必然有:∃1 < i < X, i|X
我们考虑直接枚举每个i,看他是否为X的因子
时间复杂度O(N),不符合要求
事实上我们发现,假设X是一个合数,那么必然有:X = a * b,必然有:
min(a, b) <= √X
因此我们枚举的范围可以从X变为√X
时间复杂度O(√N)
例三
求[l, r]这段区间中有多少素数
1 ≤ l ≤ r ≤ 106
一个显然的想法是利用for循环枚举[l, r]中的每一个数。然后利用例二中的知识O(√X)进行判断
整体复杂度O(N√N),不符合要求
筛法求素数
仍然考虑枚举判断每个数是否是素数,但我们这次从2开始判断。
考虑对于任意一个数x,不论x是否为素数,都有x*2,x*3,x*4...为合数。我们“筛”掉这些必然为合数的
数。
那么当我们枚举到i,i还没有被筛掉,那么i必然为素数。
时间复杂度O(NlogN)
在判断是质数的同时计数即可
例四
T次询问,每次询问[l, r]中有多少素数
1 ≤ T ≤ 105, 1 ≤ l ≤ r ≤ 106
我们用ANSL,R来表示[l, r]中有多少素数,发现ANSL,R = ANS1,R - ANS1,L-1
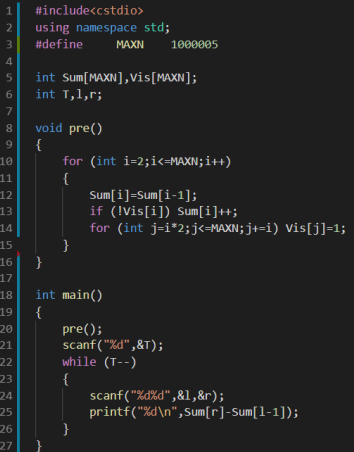
于是我们可以维护一个素数个数的前缀和Sum[i]表示[1, i]中
有多少素数
每次询问就输出Sum[r] - Sum[l - 1]即可
已知n个整数x1, x2, .., xn,以及一个整数k,k < n。从n个数字中任选k 个整数相加,可分别得到一系列的和。
例如当n = 4, k = 3,四个整数分别为3,7,12,19时,可得全部的组合与他们的和为:
3 + 7 + 12 = 22
3 + 7 + 19 = 29
7 + 12 + 19 = 38
3 + 12 + 19 = 34
现在,要求计算出和为素数的组合共有多少种。
例如上例,只有一种组合的和为素数:3 + 7 + 19 = 29
1 ≤ n ≤ 20, k < n
1 ≤ x1, x2, .., xn ≤ 5 * 106
首先我们来考虑如何枚举这样的组合。
我们用ai来表示第i个数是否被选
ai = 1表示这个数被选择了
ai = 0表示这个数未被选择
枚举过程相当于枚举了一组二进制状态
比如对于五个数1,2,3,4,5
01010表示我们选择了2,4,未选择1,3,5
在不考虑k的限制的情况下,我们枚举所有组合就相当于枚举00..00(n个0) → 11..11(n个1)
对于任意一种中间状态,0的个数+1的个数为n
我们假设这是一个长为n的二进制数,我们将它转换成十进制。
事实上就是枚举了一个数,范围是[0, 2n)
判断位置i是否为1使用位运算来完成
例六
求[l,r]中有多少数既是回文数又是素数
1 ≤ l ≤ r ≤ 107
策略一
枚举每个数,判断他是不是回文数,判断他是不是素数
时间复杂度O(N√N + NlogN)
策略二
预处理出区间所有素数,枚举素数判定是否是回文数
时间复杂度O(NlogN)
策略三
枚举区间内所有回文数,判断是否是素数
枚举回文数即枚举一个数的前一半,再手动扩展成完整的数
另外,偶数位数的回文数都必然是11的倍数,不需要枚举。
时间复杂度O(√N * √N) = O(N)
枚举的优点
简单明了,分析直观
能够帮助我们更好地理解问题
运用良好的枚举技巧可以使问题变得更简单
缺点
时空间效率低
往往没有利用题目中的特殊性质
产生了大量冗余状态
POINT2 搜索
本质上是一种枚举
搜索算法一般做一些普通的枚举不方便表达状态的情况
例题
给出一个N*N的迷宫,求从起点出发,不经过障碍物到达终点的最短距离

解决这类问题一般有两种方式
1.深度优先搜索(dfs)
2.广度优先搜索 (bfs)
前置知识
栈:后进先出的数据结构
支持的操作:
加入一个数
删除最晚加入的数
查询最晚加入的数
实现:一个数组+一个用于指向栈顶位置的变量
系统内部递归即使用了栈
例如求斐波那契数列的第n项

DFS的操作过程


遇到岔路口,随便选一个走

走不到终点就换条路
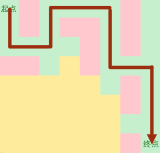
当然也可以这么走
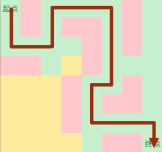
DFS的优缺点
优点:占用空间小(只需要记录从起点到当前点的路径)
代码短
缺点:获得的不一定是最优解
在图上路径非常多的时候,复杂度可能会达到指数级别
前置知识
队列:先进先出的数据结构
支持的操作:
加入一个数
删除最早加入的数
查询最早加入的数
实现:一个数组+头下标+尾下标
BFS的操作过程

开始走
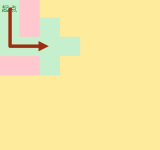
走到岔路口,都要走
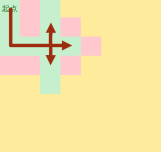
标记步数

疯狂操作
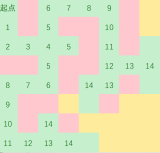
最终
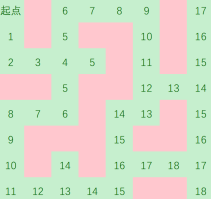
要注意这里每一个步数相同的点都是同时向外走的,所以不会出现两个路径矛盾的情况
BFS的优缺点
优点:找到答案时找到的一定是最优解
复杂度不会超过图的大小
缺点:需要维护一个“当前箭头的集合”,空间较大
DFS和BFS的区别
DFS:能走就走,走不了才回头
BFS:我全都要
应用:图的遍历
G = (V , E)被称为一张图,则其包含两部分:
1.点集|V | = n,即有n个点,标号分别为1, 2, ..., n
2.边集|E| = m,有m条边(ui, vi),表示第ui个点和第vi个点有一条边相连.
边有向边和无向边之分,(u, v)是无向边,则u能直接走到v,v能直接走到u.
图的存储结构
1.画图
2.邻接矩阵存储,用A[x][y] = 0/1表示.优点是便于加删,但是需要O(N2)的空间.
3.直接用vector存下所有的边(邻接表法).优点是空间和访问比较快,缺点是删除比较麻烦.
图的连通块
在本课中我们基本只考虑无向图.
若a沿着边走可以到b,则称a与b在同一个连通块中,称a与b连通.
显然a与b连通,b与c连通,则a与c肯定连通.
一张图可以被分成若干个两两连通的块.
图的遍历
给出一张n个点m条边的图,分别求出每个连通块.
n, m ≤ 100000.
用bfs还是dfs?
每次任选一个没有被访问过的点,然后从这个点开始bfs,找到所有和它连通的点.
时间复杂度O(N + M)(用什么方式可以让每条边被遍历常数遍?).
树
若一张图只有恰好n - 1条边,并且任意两个点之间都是连通的,则称这张图是一棵树.
树的性质:任意两点之间有且只有一条路可以相互到达.
有根树:随便给出一个点x,设x是根,然后从x开始遍历,假设你从a一步遍历到了b,则记fab = a,容易发现每个点的父亲都是
唯一的.x的父亲记为0.
给出一棵n个点的树,将它转化为有根树的形式(假定以1为根)?
N ≤ 100000
用bfs还是dfs?
理论上来说bfs和dfs都可以,但一般我们用dfs构造.
复杂度O(N).
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 1000005 #define M 20000005 #define ls tree[t].l #define rs tree[t].r #define Ls tree[t1].l #define Rs tree[t1].r #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; vector<int>v[N]; int i,j,m,n,p,k,size[N],fa[N]; void dfs(int x) { int i; size[x]=1; for (i=0;i<(int)v[x].size();++i) //遍历每条边 { int p=v[x][i]; if (fa[x]==p) continue; //如果这条边连向它的父亲,就不用管了 fa[p]=x; //否则是它的儿子,更新fa数组,然后dfs下去算 dfs(p); size[x]+=size[p]; //可以顺便计算出它向下一共有多少点 } } int main() { scanf("%d",&n); for (i=1;i<n;++i) //把所有的边加进每个点的vector当中 { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } dfs(1); }