高斯消元求解n元一次线性方程组的板子题:
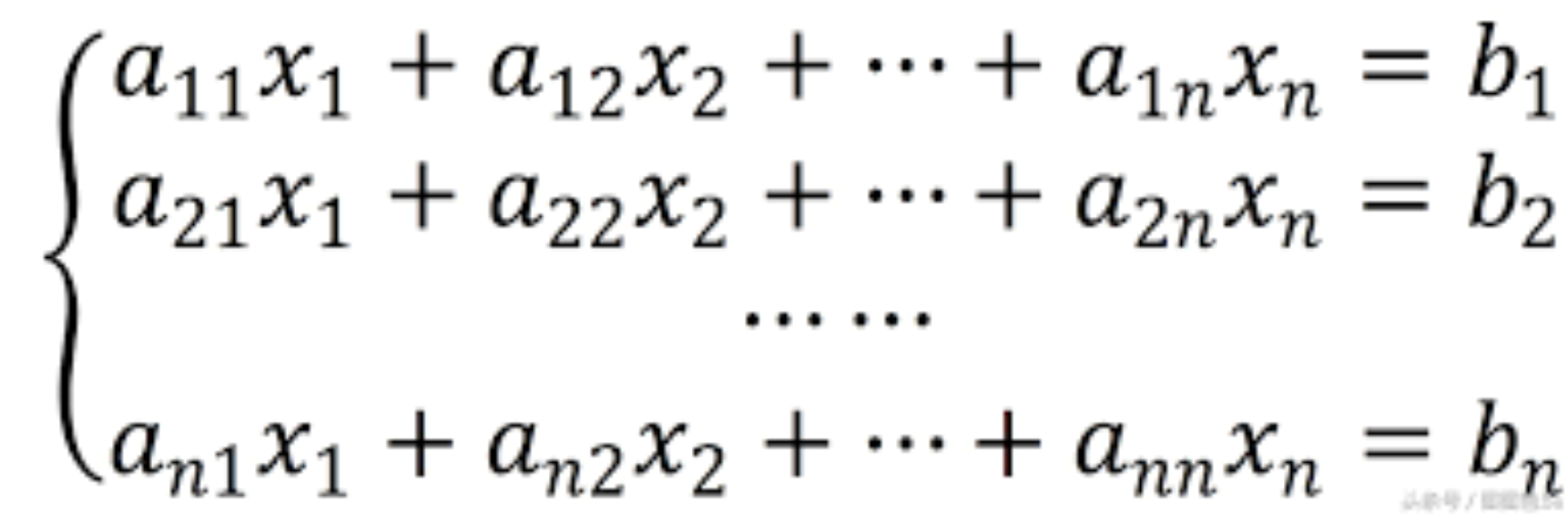
先举个栗子:
• 2x + y - z = 8-----------①
•-3x - y + 2z = -11---------②
•-2x + y + 2z = -3----------③
先将它存到矩阵中:
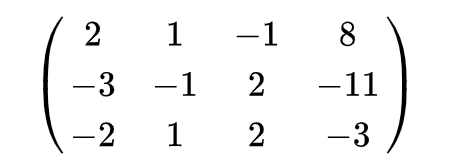
②+①* (2/3)
③+①
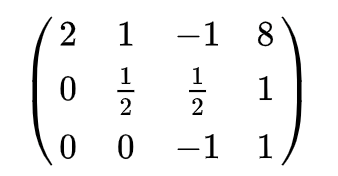
接着对①变换

得到x,y,z;
但是我们想到,如果它有在原方程中就有两个或多个方程本质上是一样的,那他不就解不出来了咩?
比如:
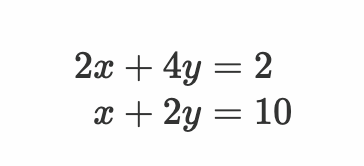
最后得出:
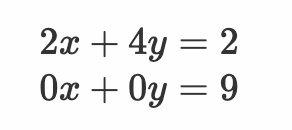
这显然就属于无解的情况
又比如:
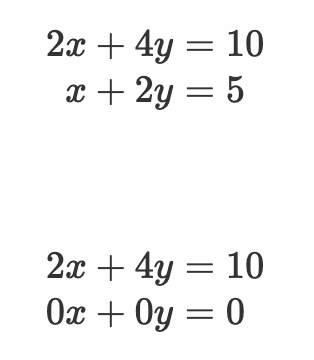
这显然就属于无穷多解的情况
这里我们引入一个定理:
一个矩阵的行列式如果不为0,方程组有唯一解,否则无解或者无穷多解
然后我们就可以通过计算行列式来判断有无解辣!
高斯消元求解线性方程组的步骤:
Step1:利用高斯消元将原矩阵(蒟阵 变为对角矩阵
具体方法:将a[i][i]除成1,这一行也进行同样的变换,用这个1去消其他的项
Step2:将对角线上的值连乘得到行列式
一个矩阵的行列式如果不为0,方程组有唯一解,否则无解或者无穷多解
在将原矩阵变为对角矩阵的过程中,线性方程组就已经消成了ax=b的形式,故只需要判断有无解即可;
求行列式:
先了解一下运算法则:传送门
行列式的计算:
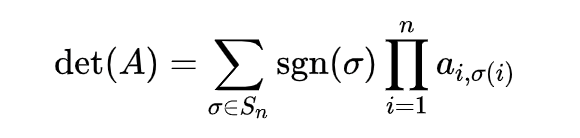
举两个例子
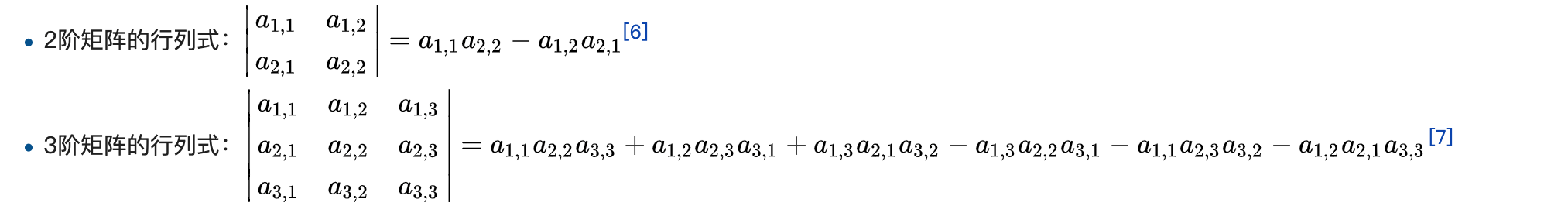
测试代码如下(注意是这里输入n是未知数个数,m是方程个数,对于这个题mn输入一样的就可以辣!):
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 #include<cmath> 6 #include<cstdlib> 7 using namespace std; 8 typedef long long ll; 9 typedef long double ld; 10 typedef pair<int,int> pr; 11 const double pi=acos(-1); 12 #define rep(i,a,n) for(int i=a;i<=n;i++) 13 #define per(i,n,a) for(int i=n;i>=a;i--) 14 #define Rep(i,u) for(int i=head[u];i;i=Next[i]) 15 #define clr(a) memset(a,0,sizeof a) 16 #define pb push_back 17 #define mp make_pair 18 #define fi first 19 #define sc second 20 ld eps=1e-9; 21 ll pp=1000000007; 22 ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} 23 ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} 24 ll read(){ 25 ll ans=0; 26 char last=' ',ch=getchar(); 27 while(ch<'0' || ch>'9')last=ch,ch=getchar(); 28 while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); 29 if(last=='-')ans=-ans; 30 return ans; 31 } 32 //head 33 int n,m; 34 double a[100][100]; 35 36 bool check(int k){ 37 if(fabs(a[k][n+1])<eps)return 1; 38 rep(i,1,n) 39 if(fabs(a[k][i])>eps)return 1; 40 return 0; 41 } 42 int main(){ 43 44 n=read();m=read(); 45 // a_i,1 a_i,2 ... a_i,n a_i,n+1 46 rep(i,1,m) 47 rep(j,1,n+1)a[i][j]=read(); 48 rep(j,1,m){ 49 rep(k,1,n+1)cout<<a[j][k]<<" "; 50 puts(""); 51 } 52 int flag=0; 53 rep(i,1,n){ 54 int t=i; 55 while(a[t][i]==0 && t<=n)t+=1; 56 if(t==n+1){ 57 flag=1; 58 continue; 59 } 60 rep(j,1,n+1)swap(a[i][j],a[t][j]);//交换两行 61 double kk=a[i][i];//每一行对角线上的值 62 rep(j,1,n+1)a[i][j]/=kk; 63 rep(j,1,m)//循环m个式子 开始消元 64 if(i!=j){ 65 double kk=a[j][i]; 66 rep(k,1,n+1) 67 a[j][k]-=kk*a[i][k];//这样就能保证正好把第i列的数除了a[i][i] 都消成0 68 } 69 puts("------------"); 70 rep(j,1,m){ 71 rep(k,1,n+1)cout<<a[j][k]<<" "; 72 puts(""); 73 } 74 } 75 if(flag){//如果flag=1,可能是 无解,也可能是无穷解 76 rep(i,1,m) 77 if(!check(i)){ 78 printf("No solution "); 79 return 0; 80 } 81 printf("So many solutions "); 82 } 83 84 }
本题AC代码:稍微改一下就行啦
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head int n,m; double a[100][100]; bool check(int k){ if(fabs(a[k][n+1])<eps)return 1; rep(i,1,n) if(fabs(a[k][i])>eps)return 1; return 0; } int main(){ n=read();m=n; // a_i,1 a_i,2 ... a_i,n a_i,n+1 rep(i,1,m) rep(j,1,n+1)a[i][j]=read(); int flag=0; rep(i,1,n){ int t=i; while(a[t][i]==0 && t<=n)t+=1; if(t==n+1){ flag=1; continue; } rep(j,1,n+1)swap(a[i][j],a[t][j]);//交换两行 double kk=a[i][i];//每一行对角线上的值 rep(j,1,n+1)a[i][j]/=kk; rep(j,1,m)//循环m个式子 开始消元 if(i!=j){ double kk=a[j][i]; rep(k,1,n+1) a[j][k]-=kk*a[i][k];//这样就能保证正好把第i列的数除了a[i][i] 都消成0 } } if(flag){ return printf("No Solution "),0; } rep(j,1,m){ printf("%.2lf",a[j][n+1]/a[j][j]); puts(""); } }