2019年x月x日,Gayly_GoatJelly_Goat大佬讲了左偏树,但窝并不会写。直到某天拿到了大佬出的左偏树
(手动分割线)
Jelly_Goat的左偏树这大概算个广告



某些题目里似乎没有说到的点:
1.大佬团被合并之后,原本抗议值较小的大佬团消失,里面的大佬进入了抗议值较大的大佬团。
2.某个大佬团消失之后,后面的大佬团的编号无需改动,也就是说暴力合并即可。
3.这题其实是个不需要并查集的板子
4.其实最开始是wz拿到了最大的巧克力,但为什么现在改成了zay呢?不得而知
好现在我们来康康左偏树是个啥
0.通(sui)俗(bian)解(kou)释(hu)
左偏树是个可并堆(当然其内部是二叉树),所以满足它的根是整棵左偏树中权值最大(或者小)的。如果画出来则是个左偏的树。最最基本的操作有合并,查询,删除堆顶。更高级的操作(比如树套树什么的)我也不会。在要求合并堆的时候肥肠之常用。
1.定义
我们定义每个节点的dist值为它与它的第一个右子树为空的子节点(不一定是儿子,也可以是孙子)的距离。
举个栗子:
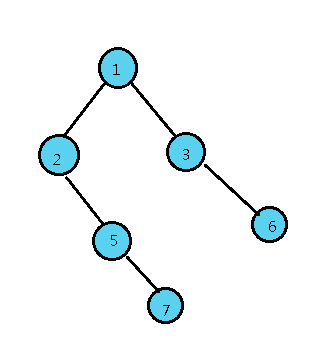
其中dist[1]=2,dist[2]=2,dist[3]=1,4号节点被我吃了,dist[5]=1,dist[6]=0,dist[7]=0
一棵左偏树需要满足以下性质:
1.根节点的权值最大
2.每个节点的左儿子的dist值大于等于右儿子的dist值(也就是说某个节点如果只有一个儿子,那就只有左儿子),这也是为什么这个东西叫左偏树
2.左偏树的一些性质
1.它是个堆
2.我们可以发现一个节点的dist值是min(它的左儿子的dist,它的右儿子的dist)+1,由于左偏树上左儿子的dist一定不小于右儿子的dist,所以一个点的dist值为它的右儿子的dist+1
3.显然一个左偏树的任意一个子树也是左偏树(当然一个空树也可以是左偏树)
3.左偏树的基本操作
合并
按照左偏树的性质,我们要选出权值最大的作为根(以下都按大根堆讲,小根堆同理可得)。如果此时有多个最大值,则选择dist比较大的作为根。
那根的儿子呢?我们前面说过左偏树的任意一个子树也是左偏树,所以我们可以像处理大的左偏树一样来处理它。这样就变成了不断递归选根,也就是合并。
代码也很好写
int merge(int x,int y)
{
if(!x||!y) return x+y;//到了叶子节点,返回那个存在的节点
if(co[x]<co[y]) swap(x,y);//co[x]表示x的权值
son[x][1]=merge(son[x][1],y);//考虑y可能是x的左儿子,也可能是y的右儿子的某个子节点
if(dist[son[x][0]]<dist[son[x][1]])swap(son[x][0],son[x][1]);
dist[x]=dist[son[x][1]]+1;
return x;
}
删除
删除某个左偏树的根节点,只需要把它的左右儿子合并即可.当然也要根据不同的题目要求来对被删去的节点进行一番操作。在(Jelly_Goat)的题目里需要记录这个大佬已经被zay制裁了,并且更新第x个大佬团的权值。也要注意这个大佬团是否为空
int del(int x)
{
int rt=merge(son[x][0],son[x][1]);
if(rt) co[x]=co[rt];//更新权值
else sl[x]=1;//这个团它死了
}
查询
在(Jelly_Goat)的题目里,直接输出x的权值即可,因为它问的是第x个团的最大值,而不是x所在的团的最大值。如果是第二种问法,写个并查集即可。(也就是左偏树板子题)
咱还是上个全套代码叭
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<vector>
#define pa pair<int,int>
using namespace std;
typedef long long ll;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}//可能有些毒瘤题会卡的快读
const int wz=2147483647;//wz大佬的巧克力(别问我为什么不是zay)
int n,co[100009],m,son[100009][2],dist[100009];
bool sl[100009];
int merge(int x,int y)//合并
{
if(!x||!y) return x+y;
if(co[x]<co[y]) swap(x,y);
son[x][1]=merge(son[x][1],y);
if(dist[son[x][0]]<dist[son[x][1]])swap(son[x][0],son[x][1]);
dist[x]=dist[son[x][1]]+1;
return x;
}
int del(int x)
{
int rt=merge(son[x][0],son[x][1]);
if(rt) co[x]=co[rt];
else sl[x]=1;
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
co[i]=read(),co[i]=wz-co[i];
while(m--)
{
int cz=read();
if(cz==1)
{
int x=read();
if(sl[x])printf("-1
");//如果这个团死了就输出-1
else printf("%d
",co[x]);
}
if(cz==2)
{
int x=read();
del(x);
}
if(cz==3)
{
int x=read(),y=read();
int rt=merge(x,y);
if(rt==x) sl[y]=1;//让抗议值较小的团死去
else sl[x]=1;
}
}
}
嗯,没了
接下来我们愉快的打开左偏树板子,发现要写并查集
题面如下:



我们发现,如果直接进行路径压缩是会wa的。那我们不进行路径压缩。

噫好我没了。(bushi
最后一个点是个长达99999的链,T到飞起。这时候我们应该用(O(n))randomshuffle一下 显然我不会显然我们应该考虑考虑路径压缩之后怎么让它AC。
我们发现,路径压缩过后,应该被删掉的点的左右儿子合并后的根的父亲还是应该被删掉的根。如果我们草率的把应该删掉的点的父亲设为-1,那么整个堆就没有根了。为了保证正确性,要把fa[被删掉的点]改为新的根。
其他操作和上面差不多,详情请见注释
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<vector>
#define pa pair<int,int>
using namespace std;
typedef long long ll;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
const int wz=2147483647;
int n,co[100009],m,son[100009][2],dist[100009];
int dui[100009];//dui[i]就相当于并查集里的fa
int find(int x)
{
if(x==dui[x])return x;
dui[x]=find(dui[x]);
return dui[x];//写丑了的路径压缩
}
int merge(int x,int y)
{
if(!x||!y)return x|y;
if(co[x]>co[y]||(co[x]==co[y]&&x>y)) swap(x,y);//注意交换时考虑到顺序问题
son[x][1]=merge(son[x][1],y);
if(dist[son[x][0]]<dist[son[x][1]])swap(son[x][0],son[x][1]);
dist[x]=dist[son[x][1]]+1;
dui[son[x][0]]=x;
dui[son[x][1]]=x;
return x;
}
int del(int x)
{
dui[son[x][0]]=son[x][0];
dui[son[x][1]]=son[x][1];
dui[x]=merge(son[x][0],son[x][1]);//把被删除的点的父亲设为新根
son[x][0]=0;son[x][1]=0;
co[x]=-1;//权值置为-1
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
co[i]=read(),dui[i]=i;
while(m--)
{
int cz=read();
if(cz==1)
{
int x=read(),y=read();
if(co[x]==-1||co[y]==-1||dui[x]==dui[y])continue;
int rt=merge(find(dui[x]),find(dui[y]));
dui[rt]=rt;
}
if(cz==2)
{
int x=read();
if(co[x]==-1)
{
printf("-1
");continue;
}
int qwq=find(x);
printf("%d
",co[qwq]);
del(qwq);
}
}
}