前言
显然qtree系列都是树链剖分辣
发现自己没有专门整理过树链剖分耶
辣么就把这篇博客魔改成树链剖分好辣(貌似除了树剖也没什么好写的)
正文
废话了辣么多终于开始了
一.树剖怎么写鸭
二.树剖有什么用鸭
三.qtree3题解
树剖怎么写鸭
树剖,顾名思义就是把树 剖成一条一条的东西,然后把一棵树搞成一个序列。 咋剖? 对于树上的每个节点,我们定义它的儿子中,有着最大子树的儿子就是重儿子(因为它画出来显得比较重),然后我们从根节点开始,一直走重儿子,就走出来一条重链。那些不在重链上的边怎么办呢?我们给他们起个名字,叫轻边。处理重儿子
void dfs1(int u,int fa)
{
dep[u]=dep[fa]+1;//这是深度
par[u]=fa;
sz[u]=1;
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(to==fa)continue;
dfs(v,u);
sz[u]+=sz[v];
if(sz[son[now]]<sz[v])son[now]=v;
}
return;
}
我们要把树搞成一个序列,所以要给每个节点一个编号dfn。dfn就是dfs序,dfn[i]也就是节点i是在dfs时第几个被遍历到了。在dfs时,先走重儿子,再走其他儿子。这样所有重儿子的dfn就是连续的,方便后面进行操作(why?)
emm蒟个栗子
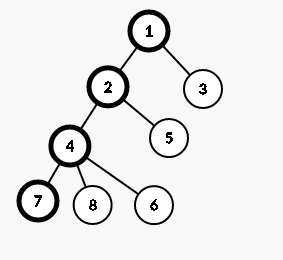
其中加粗的点构成一条重链(最下面的点也可以是8,9)
搞重链和轻边
void dfs2(int u,int fa)
{
cnt++;
dfn[u]=cnt;
id[cnt]=u;//记录dfn值对应的原来的编号
if(son[fa]==u)top[u]=top[fa];
else top[u]=u;
if(!son[u])return ;
dfs2(son[u],u);
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(v!=fa&&v!=son[u])
dfs2(v,u);
}
}
辣么我们搞这个重链到底有什么用呢
良(du)心(liu)出题人肯定会搞一些树上的询问对不对?树上的询问一般都要涉及两个点之间的路径对不对?要搞路径就要找lca对不对?这时候就要用到重链和轻边了。
对于每一条链都会有一个链的顶部(一条轻边自己就是一条链),我们可以一条链一条链的往上跳,也就是每次都跳到当前所在链的顶部再往上一个点(以便找下一个顶部)。这样,当再跳一步,两个点所在链的顶部相同时,就说明lca在这条链中。
再蒟个栗子

现在我们要求6和8的lca
图中加粗的点是重儿子
6所处的链的顶端是1,8的顶端是10
这里我们先跳顶端比较深的那个点,也就是跳8
如果跳这一步:
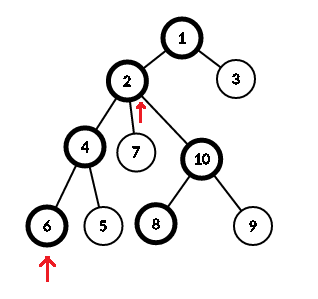
这时候发现2和6的顶端是一样的,说明6和8的lca肯定在1->2->4->6这条链中
那么2和6中靠近根的点就是lca,在这里就是2。
找到了lca之后呢?再从lca往下跑?
不,不需要这么麻烦。
我们在上面处理dfn的时候,处于同一条重链上的点的dfn是连续的,也就是构成了一个区间。这个区间里的信息可以在线段树上维护。所以我们在找lca的时候,同时将这段区间的信息统计到答案里面。所以我们就切掉了查询操作。
查询代码(以求点权之和为例)
int sum(int x,int y)
{
int ans=0;
while(top[x]^top[y])//top[x]!=top[y]
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
ans+=query(1,1,n,dfn[top[x]],dfn[x]);//query就是线段树的query辣
x=par[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
ans+=query(1,1,n,dfn[x],dfn[y]);
return ans;
}
什么?线段树怎么写?点这里qwq至于线段树维护什么因题而异,这里就不多说辣。
树剖是个什么玩意&有什么用
树剖可以对树进行操作,然后把树搞成一个区间,再加上线段树等数据结构的辅助,从而让我们的暴力跑的更快(港真树链剖分其实是一个优化暴力)
经典类型(可能以后会补充):原本序列上的操作被duliu出题人搞到了树上;给出的图是一棵树而且还会神烦的改边权
qtree3的题解
[传送](https://www.luogu.org/problem/P4116)  其实qtree系列的难点在于我们要在线段树上维护什么。
对于这道题,我们要在线段树上维护什么呢?
当然是当前节点代表的区间中第一个黑点的dfn值辣。(初始值全部为inf)
然后结合线段树和树剖的板子这道题就写完了
一个大小坑:
我们在树剖的时候建的是双向边,所以注意#####数组要开到2e5!!!!!
鉴于luogu是个神奇的网站,不开2e5的边的评测结果是这样的:

emmmm当时真的以为是query无限递归什么的然后愣是WA了一个月没调出来,某天吃饭的时候突然醒悟边tm开小了
Code:
#include<iostream>
#include<queue>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define pa pair<int,int>
typedef long long ll;
using namespace std;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
const int inf=21474836;
int fir[300009],dfn[100009],son[100009],par[100009],top[100009];
int n,q,dep[100009],cnt,head[100009],sz[100009];
int tim,idx[100009];
struct E{
int to,nxt;
}ed[300009];
void add(int fr,int to)
{
cnt++;
ed[cnt].to=to;
ed[cnt].nxt=head[fr];
head[fr]=cnt;
}
void dfs1(int now,int fa)
{
dep[now]=dep[fa]+1;
par[now]=fa;
sz[now]=1;
for(int e=head[now];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(v==fa)continue;
dfs1(v,now);
sz[now]+=sz[v];
if(sz[v]>sz[son[now]])
son[now]=v;
}
return ;
}
void dfs2(int now,int fa)
{
++tim;
dfn[now]=tim;
idx[tim]=now;
if(son[fa]==now)
top[now]=top[fa];
else top[now]=now;
if(!son[now]) return;
dfs2(son[now],now);
for(int e=head[now];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(v!=son[now]&&v!=fa)
dfs2(v,now);
}
// printf("dfn[%d]=%d
",now,dfn[now]);
}
void build(int k,int l,int r)
{
if(l==r)
{
fir[k]=inf;
return ;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
fir[k]=inf;
}
void chg(int k,int l,int r,const int &v)
{
if(l==r)
{
if(fir[k]==inf) fir[k]=l;
else fir[k]=inf;
return ;
}
int mid=(l+r)>>1;
if(v<=mid) chg(k<<1,l,mid,v);
else chg(k<<1|1,mid+1,r,v);
fir[k]=min(fir[k<<1],fir[k<<1|1]);
}
int query(int k,int l,int r,const int &x,const int &y)
{
if(x<=l&&r<=y)
{
return fir[k];
}
int mid=(l+r)>>1;
int rtn=inf;
if(x<=mid) rtn=min(rtn,query(k<<1,l,mid,x,y));
if(mid<y) rtn=min(rtn,query(k<<1|1,mid+1,r,x,y));
return rtn;
}
int qfir(int x)
{
int y=1;
int rtn=inf;
while(top[y]^top[x])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
rtn=min(rtn,query(1,1,n,dfn[top[x]],dfn[x]));
x=par[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
rtn=min(rtn,query(1,1,n,dfn[x],dfn[y]));
return rtn;
}
int main()
{
n=read();q=read();
for(int i=1;i<n;i++)
{
int fr=read(),to=read();
add(fr,to);
add(to,fr);
}
dfs1(1,0);
dfs2(1,0);
build(1,1,n);
for(int i=1;i<=q;i++)
{
int cz=read(),v=read();
if(cz==0)
chg(1,1,n,dfn[v]);
else
{
int ans=qfir(v);
printf("%d
",((ans==inf)?-1:idx[ans]));
}
}
}
好了在结尾安利一道树剖模板题