7.9刚考了,今天又考ρωρ



这里undo可以撤销undo操作emm可真是神奇
先说一下50pts:直接开数组模拟

#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<stack> using namespace std; int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,u; char zs[100009]; int main() { freopen("type.in","r",stdin);//考试不要忘了 freopen("type.out","w",stdout); n=read(); for(int i=1;i<=n;i++) { char cz=getchar(); while(cz!='T'&&cz!='U'&&cz!='Q')cz=getchar(); if(cz=='T') { char ty=getchar(); while(ty==' '||ty==' '||ty==' ')ty=getchar(); zs[++u]=ty; } if(cz=='Q') { int num=read(); if(num>u)printf(" "); else printf("%c ",zs[num]); } if(cz=='U') { int num=read(); u-=num; } } }
来我们考虑剩下那50怎么拿
当然是用可持久化线段树或者主席树做了
既然可以撤销撤销操作,那么我们可以把每一步操作后的状态都记录下来。在这里用栈模拟还是很方便的,所以我们就可以开一堆栈,第i个栈表示进行完第i次修改操作(不包含查询操作)后的状态记录下来,就像下面这样。

注意这是4个不同的栈
这样我们就可以知道进行完当前操作,栈长什么样子了
不过.....空间爆炸警告
操作几次就有几个栈,操作1e6次不是RE就是MLE(还可能TLE,或者交出个七彩祥云)。
那我们究竟把空间浪费在哪了呢?
数据很有可能一直在插入字符,当插入了几百个之后开始不断的撤销撤销撤销。这时候我们按照上面的方法,每次都要拷贝几百个不会被影响到的字符。这在空间和时间上都造成很很很大的浪费。
那我们就偷个懒,不拷贝了。我们维护一个链表当前的顶部,如果有撤销操作,就让当前这个顶部和x步(就是撤销的步数)前的那个链表顶部相同。
画个图吧
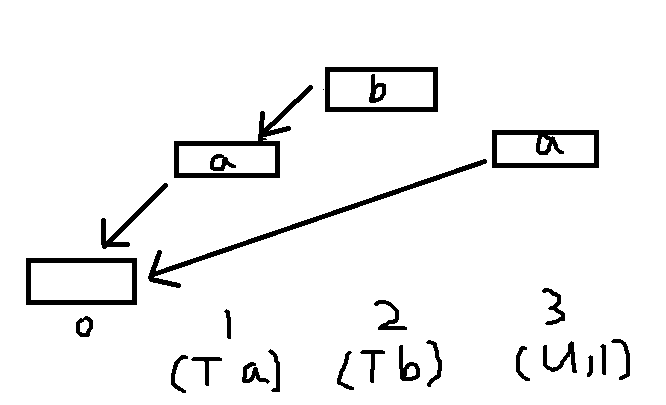
数字是第几步,数字下面是这一步的操作。
这样插入和删除都没有问题了。接下来就是查询了。emmm好像复杂度炸了?!
上面的查询复杂度是O(top-x)的(x就是第几个数),显然如果数据中查询过多会TLE对吧。
so我们下一步是优化查询。
数组查询很快,但是插入,撤销很慢,链表插入,撤销很快,但查询很慢,可不可以让它们中和一下?
这里有个神奇的东西叫块状数组,其实就是个链表。之前的链表每个节点只能存一个数,现在我们让每个节点存B个数(这里的B是自己确定的,wz用提交答案进行二分最后认为在这道题里面B=2000左右比较好)(wz神仙还说这题B=√¯n)
总之我们这里让B=√n好了。
插入和撤销还是上面的思路,只是当插入的时候,我们判断当前这个块有没有满,没满:直接在后面插入,满了:新建一个块,再插入。
查询:我们知道了x和一个块的大小B,则我们可以先跳过x/B个块,然后再从x所在的块里面寻找x,这样比一个一个往后找快多了。不过这里我们还是倒着找的,所以x=size-x(size是当前字符的总个数)
那这个题除了不会写代码是不是就没有任何的问题了?
好的我们直接看wz神仙的代码
#include <cmath>//接下来是同zay一样令人窒息的指针 #include <cstdio> #include <cstring> template <class T> inline void read(T &num) { bool flag = 0; num = 0; char c = getchar(); while ((c < '0' || c > '9') && c != '-') c = getchar(); if (c == '-') { flag = 1; c = getchar(); } num = c - '0'; c = getchar(); while (c >= '0' && c <= '9') num = (num << 3) + (num << 1) + c - '0', c = getchar(); if (flag) num *= -1; } inline void read(char &c) { do { c = getchar(); } while (c == ' ' || c == ' ' || c == ' '); } template <class T> inline void output(T num)//神仙的快输 { if (num < 0) { putchar('-'); num = -num; } if (num >= 10) output(num / 10); putchar(num % 10 + '0'); } template <class T> inline void outln(T num) { output(num); putchar(' '); } template <class T> inline void outps(T num) { output(num); putchar(' '); } template <class T> inline T max(T a, T b) { return a < b ? b : a; } const int N = 100000; int n, B; struct node { char *s;//s是一个字符串 int now, pc;//now是存到了当前块的第几个位置,pc是统计当前有几个块 node *pre;//pre是前驱 node() { now = pc = 0; s = new char[B]; pre = NULL; } void copy(node *src)//拷贝一个一毛一样的节点 { now = src->now; pc = src->pc; pre = src->pre; for (int i = 0; i < now; i++) { s[i] = src->s[i]; } } } * head[N]; int lst; void append(char x)//插入 { if (head[lst]->now == B) { head[++lst] = new node; head[lst]->pre = head[lst - 1]; head[lst]->pc = head[lst - 1]->pc + 1; head[lst]->s[head[lst]->now++] = x; } else { head[++lst] = new node; head[lst]->copy(head[lst - 1]); head[lst]->s[head[lst]->now++] = x; } } char query(int x) { int siz = head[lst]->now + head[lst]->pc * B;//siz就是size,当前元素的个数 x = siz - x + 1; if (x <= head[lst]->now) { return head[lst]->s[head[lst]->now - x]; } x -= head[lst]->now;//先跳过最后一个块 node *now = head[lst]->pre; while (x > B)//一直跳块 { now = now->pre; x -= B; } return now->s[B - x]; } int main() { read(n); B = sqrt(n); head[0] = new node; for (int i = 1; i <= n; i++) { char op; read(op); if (op == 'T') { char x; read(x); append(x); } if (op == 'U') { int x; read(x); head[lst + 1] = head[lst - x];//节点是一毛一样的 lst += 1; } if (op == 'Q') { int x; read(x); putchar(query(x)); putchar(' '); } } }


看到这一个题,我们想起了昨天那到斐波那契数列。怎么做呢?打表啊。
但是这个题就算打出来表也看不出来神马规律
我们还是用正常的思维推理一下吧
设f[i][j]为n=i,k=j时的答案
我们假设我们已知f[n-1][k],这时候我们需要插入一个n。应该怎么插入呢?
我们插入的地方有4中可能
①:在序列的首部
②:在序列的尾部
③:插入在n-1形成的序列的''>''处
④:在''<''处
①:原来的''>''数量+1,''<''数量不变(即k不变)
②:''<''数量+1(k+1)
③:由于插在原来的''>''处,且n>1到n-1中的任意一个数,所以''<''数量+1,''>''数量不变,即k+1
④:与③相反,''<''数量不变,''>''数量+1,k不变
这样,f[n][k]就可以由f[n-1][k]和f[n-1][k-1]得到
由f[n-1][k]转移时,要么是①,要么是④。f[n-1][k]有几个地方是小于号,就要乘几。f[n-1][k]当然有k个地方是小于号喽(第二维都是k了),再加上在首部插入,所以f[n-1][k]对答案的贡献是f[n-1][k]*(k+1)
由f[n-1][k-1]转移时,情况有②和③。由于n-1个数有n-2个空,其中小于号有k-1个,所以大于号就是(n-2-(k-1))=n-k个
综上,f[n][k]=f[n-1][k]*(k+1)+f[n-1][k-1]*(n-k)
代码:
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<stack> using namespace std; int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,k,dp[1009][1009]; const int mod=2012; int main() { freopen("num.in","r",stdin); freopen("num.out","w",stdout); n=read();k=read(); if(k==n-1) { printf("1");return 0; } for(int i=1;i<=n;i++)//由暴力打表可得dp[i][0]=1 dp[i][0]=1; for(int i=1;i<=k;i++) { for(int j=1;j<=n;j++) { if(j<i)continue; dp[j][i]=dp[j-1][i]*(i+1)+dp[j-1][i-1]*(j-i); dp[j][i]=(dp[j][i]+mod)%mod; } } printf("%d",dp[n][k]); }



看到这个题,依旧没有什么想法emmmm
所以这就是我爆搜只有10分的理由
我们直接来看正解吧
这道题是真•dp
因为是真•dp,所以我们要倒着dp
我们发现这个在当前星球的决策会影响到下一个星球,据大佬说这叫有后效性,so我们可以倒着dp。
看这几个式子

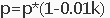


好像不管我们干啥事都有p的事。你看这个p是不是很烦?那我们就把p都提出来,最后再乘进去。
那究竟怎么dp呢?对于每一个星球,我们有两种选择。一:进行一番操作。二:什么也不做。用dp[i]表示在i星球得到的最大金钱,那dp[i]肯定是在上面两种选择中选择一个金钱最大的。
什么都不做,那肯定就是dp[i+1](我们倒着dp)
每个星球都有类型,我们考虑如果当前星球是类型1,则开采获得的金钱为a[i],由于钻头的损坏,dp[i+1]的贡献就变成了dp[i+1]*(1-0.01k)(注意这里已经将p提出来了,就不管p的事了)。那么开采就是a[i]+dp[i+1]*(1-0.01k),dp[i]=max(dp[i+1],a[i]+dp[i+1]*(1-0.01k))
如果当前星球是类型2,则维修消耗的金钱是b[i],钻头经过维修,dp[i+1]的贡献就是dp[i+1]*(1+0.01c),所以dp[i]=max(dp[i+1],dp[i+1]*(1+0.01c)-b[i])
最后dp[1]*w就是答案(我们之前提出了p,最后要乘回去)
代码:
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> using namespace std; int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,w,c,k,a[100009]; double dp[100009]; int zy[100009]; int main() { freopen("exploit.in","r",stdin);//别忘了加!!! freopen("exploit.out","w",stdout); n=read();k=read();c=read();w=read(); for(int i=1;i<=n;i++) { zy[i]=read(); a[i]=read(); } double kk=1-0.01*(double)k; double cc=1+0.01*(double)c; for(int i=n;i>=1;i--) { if(zy[i]==1) dp[i]=max(dp[i+1],dp[i+1]*kk+a[i]); else dp[i]=max(dp[i+1],dp[i+1]*cc-a[i]); } printf("%.2lf",1.0*dp[1]*w); }
