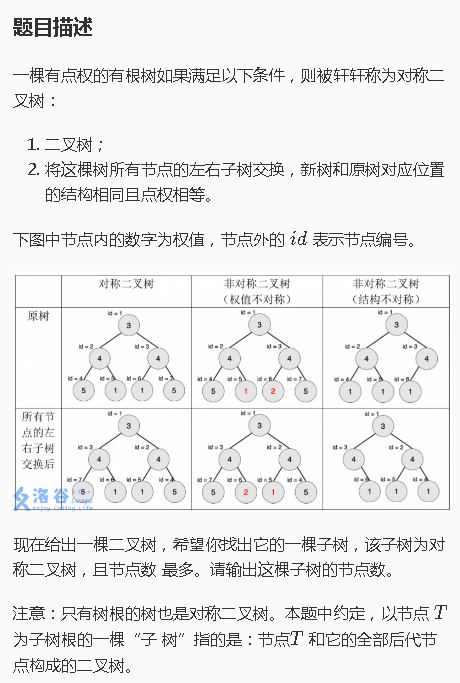




题目说了那么多,到底什么是对称二叉树呢?
就是关于根节点左右镜面对称的二叉树辣。
当然,一棵对称二叉树的子树不一定是对称二叉树,就比如下面这个
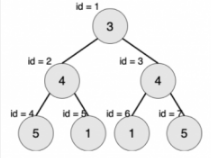
它是对称二叉树,但是对于它的子树
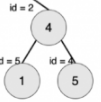 这并不是对称二叉树
这并不是对称二叉树
那怎么判断对称二叉树呢?
对于每一个节点,都进行一次搜索。
在搜索之前,我们可以处理出对任意的一个节点u,以u为根的子树的节点数,即以u为根的子树的大小。
搜索:
首先,如果当前节点 i 的左右子树的节点数不相等,或者是左右儿子的权值不相等,就可以不用继续搜索了,直接返回。
维护两个指针,一个指针指向i的左儿子的右儿子,一个指向右儿子的左儿子,然后再反过来。因为能到这一步,就说明i的左右儿子的权值相等,且左右子树大小相同,就不用管u,v了。
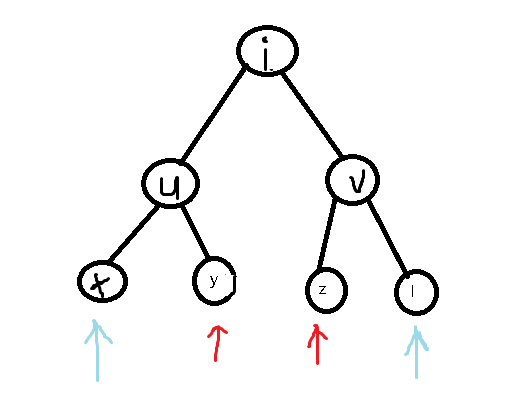
红色为第一次比较时指针的指向,蓝色为第二次比较时指针的指向。
如果y,z的权值相等,子树大小相同,x,l权值相等,子树大小相同,则继续向下搜索,否则就直接返回。(这里考虑子树大小是因为可能出现下面这种情况)
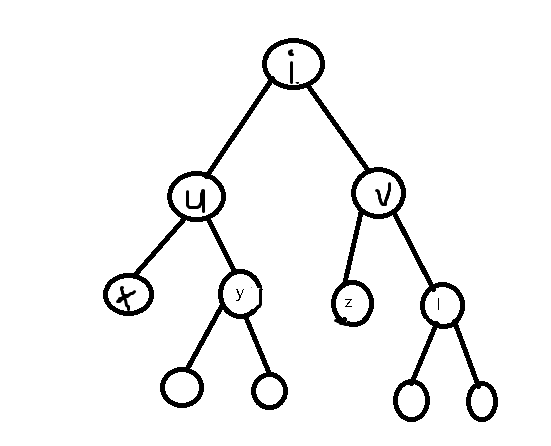
这样虽然u,v的子树大小相同,但是y,z的子树大小不同,所以要考虑子树。
%%%wxl用十几分钟讲完了这道题
代码:
#include <bits/stdc++.h> using namespace std; int n,son[1000009][3],node[1000009],size[1000009]; int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } f?x=-x:x=x; return x; } void dfs(int x)//预处理子树大小(size) { size[x]=1; if(son[x][0]!=-1) { dfs(son[x][0]); size[x]+=size[son[x][0]]; } if(son[x][1]!=-1) { dfs(son[x][1]); size[x]+=size[son[x][1]]; } } bool check(int u,int v)//一个长成check的搜索 { if(u==-1&&v==-1)return true;//注意如果左右儿子都不存在,那这是个叶节点,也是对称二叉树 if(size[u]!=size[v])return false; if(u!=-1&&v!=-1&&node[u]==node[v]&&check(son[u][0],son[v][1])&&check(son[u][1],son[v][0]))//分别对上图的红色指针所对应的节点和蓝色指针所对应的节点进行判断 return true; return false;//其他一些神奇的情况就直接返回false了 } int main() { n=read(); for(int i=1;i<=n;i++) node[i]=read(); for(int i=1;i<=n;i++) { son[i][0]=read(); son[i][1]=read(); } dfs(1); int ans=-1; for(int i=1;i<=n;i++) { if(check(son[i][0],son[i][1]))//对所有的对称二叉树的节点取最大值 ans=max(ans,size[i]); } printf("%d",ans); }