推荐生要凉辽
这可能是我更新的最后一篇博客
代码什么的有时间再说吧,先讲思路。(已搞定前三题代码)

首先先看一下线段覆盖题。我们有一个区间,要用线段覆盖整个区间。
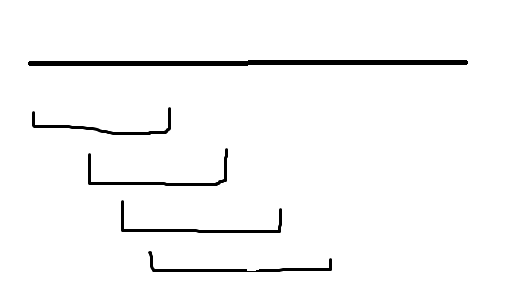
这个是线段的覆盖简图。我们如何选取最少的线段来覆盖整个区间呢?先将右端点排序,再将左端点贪心一下。
比如:
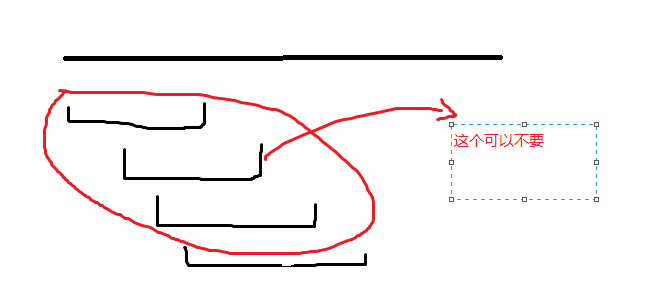
但在这个题里面覆盖的是格子,不一定连续。这就比较复杂了,我们要想点办法。我们线段覆盖解决的是格子连续的情况。所以我们要先证明第一行每个格子里的蓄水池覆盖第n行的格子是连续的。

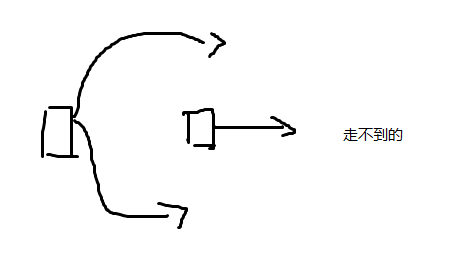
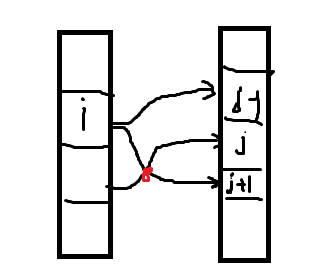
如果从i无法流到j,而能流到j-1和j+1,从别的城市可以流到j,那么这两条路线一定有一个交点,那么i也可以从这个交点流到j,这与条件矛盾。
然后这就是一个线段覆盖的问题了。因为在第1行的城市对第n行的城市覆盖的区间是连续的,就相当于在第n行进行线段盖。
我们解决能否到达时,就用dfs/bfs求一遍,顺便把第一行每个城市覆盖的第n行城市求出来,然后进行线段覆盖。
这样会T一个点,所以我们要有个优化:第一行只有比两边都搞的点才进行搜索,如果有一边比这个点高,那这个点所覆盖的区域肯定在比这个点高的子集里面。
以及注意一下n=1的情况,下面代码里会讲
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<queue> using namespace std; int n,m,a[501][501],k,ans,ans2; int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1}; struct xianduan
{//处理线段 int l, r; xianduan()//构造函数(结构体初始化) {l=2147483647; r=-1; } }xd[550];//记录第一行每个点覆盖的第n行的区间 bool vis[501][501],vis2[501];//vis记录在一次搜索中走过的点,vis2记录最后一行被覆盖的点 bool check() {bool c=1; for(int i=1;i<=m;i++)//判断最后一行是否都被覆盖 { if(!vis2[i]){c=0;ans2++;}//如果有没被覆盖的,就统计个数 } return c; } struct dl{ int x,y; dl(int xx,int yy):x(xx),y(yy){}//构造函数*2 }; bool hf(int x,int y,int xx,int yy)//广搜时判断能不能走 { if(xx<1||yy<1||xx>n||yy>m)return 0; if(a[xx][yy]>=a[x][y])return 0; if(vis[xx][yy])return 0; return 1; } queue <dl> q; void bfs(int st)//广搜模板 { if(a[1][st]<a[1][st-1]||a[1][st]<a[1][st+1])return ; memset(vis,0,sizeof(vis));//每次搜索记得清空,不然可能会出现什么意外 vis[1][st]=1; while(!q.empty()) {dl ex=q.front(); q.pop(); for(int i=0;i<4;i++) {int xx=ex.x,yy=ex.y; xx+=dx[i];yy+=dy[i]; if(hf(ex.x,ex.y,xx,yy)) {vis[xx][yy]=1; q.push(dl(xx,yy)); if(xx==n) {if(yy>xd[st].r){xd[st].r=yy;}//记录xd[i] if(yy<xd[st].l){xd[st].l=yy;} vis2[yy]=1;//因为vis每次都要清空,所以才用vis2来记录 } } } } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[i][j]); for(int i=1;i<=m;i++) bfs(i); if(check()) {int left=1,r_max=0; while(left<=m) { for(int i=1;i<=m;i++) {if(xd[i].l<=left)r_max=max(r_max,xd[i].r); } ans++; left=r_max+1; } printf("1 %d ",ans); } else { if(n==1)printf("1 %d ",ans2);//n=1时的特判。因为当n=1时,每次出队的点的vis2并不会被标记,所以没有标记的点(1,j)就是建蓄水池的点 else printf("0 %d ",ans2); } }
不枉我肝了近90行,wa了3次

我们先枚举第二个客栈j,找到j前面的第一个(从右往左)价格合理,颜色符合要求的客栈i。那么在i前面,颜色和i一样的客栈的数量+1就是当前j的方案数,如果在i后面,j前面还有颜色相同的客栈,那么这些客栈的方案数与j相同。

上面的式子在说些什么呢?就是当前以i为右端点的方案数,如果当前i客栈这种颜色出现的最大的地方(不包括i)k要比当前价钱合理的最大的地方t位置靠后的话,就是k的方案数。
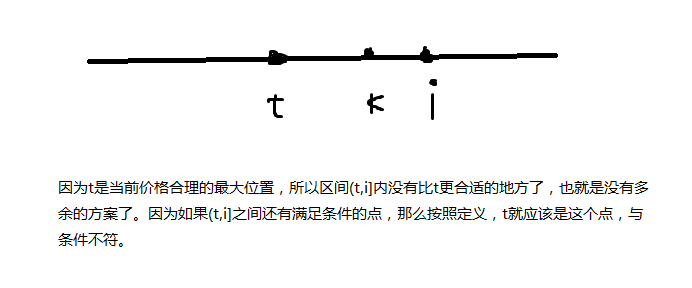
当出现这种情况时:
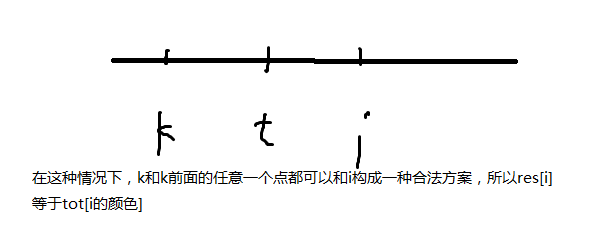
更多细节请见代码:
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> #include<queue> const int MAXN=2000001; using namespace std; int p,k,n,pre[MAXN],pos[51],tot[51],res[MAXN]; struct kezhan{ int col,mon;//col是coler,mon是money }a[MAXN]; int main() { scanf("%d%d%d",&n,&k,&p); for(int i=1;i<=n;i++) {scanf("%d%d",&a[i].col,&a[i].mon); if(a[i].mon<=p)pre[i]=i;//因为这里每个下标i对应的都是不一样的数,所以可以在输入中预处理 else pre[i]=pre[i-1]; } for(int i=1;i<=n;i++) { if(pre[i]<pos[a[i].col])//先dp,再统计tot和pos res[i]=res[pos[a[i].col]]; if(pre[i]>=pos[a[i].col]) res[i]=tot[a[i].col]; pos[a[i].col]=i; tot[a[i].col]++; } long long ans=0; for(int i=1;i<=n;i++)//最后答案是每个i作为右端点的方案数的和 ans+=res[i]; printf("%lld",ans); }

交了6次才A,嘤嘤嘤
首先考虑并没有加速器的情况。
设wait[i]表示到i最晚的游客到达的时刻,设arrive[i]表示车到i点的时刻。
则arrive[i]=max(arive[i-1],wait[i-1])+d[i](d[i]就是路程)
现在我们加上加速器。
加速器可以减少距离,但并不能减少游客的到达时间,所以当游客的到达时刻大于汽车的到达时刻的时候,使用加速器就没有意义了。我们要让加速器有效,就选取arrive[i]比wait[i]大的点,进行加速,然后重复上面的过程,一直到加速器用完或是没有满足条件的边为止。
因为代码的维护不会写(树状数组优化复杂度神马的)然后翻洛谷题解,有了些新的收获。
1.这个题的维护不需要优化,因为o(n^2)也能过
2.这里贪心的是造福最多人民群众的区间(可能上课没好好听漏了点思路qwq我错惹)
代码什么的可能1个月之后才会出吧。
先理一理思路。
首先,我们预处理出车在每个点的等待时间。
递推计算每个点的arrive,并且统计在哪里会产生arrive大于wait并且用了加速器后能造福最多的人民群众,将这一段区间进行维护,一直到加速器用完为止。
维护的话,因为对一个[i,i+1]使用加速器后,可能影响到后面的arrive。如果后面的arrive>wait,就说明这里使用加速器会影响后面,否则不会。就跳出循环。
我们看到题,就会发现di的定义别扭的一批,所以我们改一下,有助于后面我们乱搞。
我们把di的定义改为从i-1到i的距离,读入就改为:
for(int i=2;i<=n;i++) scanf("%d",&d[i]);
注意是从i=2开始读入。
我们要选择造福人数最多的点,所以我们边读入边处理到达每个点的人数。在使用加速器的时候,每次都从头开始更新造福人最多的点(注意memset(不写memset爆0警告)),选出最多的点进行更新。
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> using namespace std; int goal[1002],d[1002],m,k,n,wait[1002],arr[1002],yx[1002],max_i,max_yx;//yx[i]是选择在i-1到i的距离-1,造福的人数,arr[i]为到达第i个点的时刻,wait[i]是每个点要等多久 struct c{ int time,st,aim; }ck[100001]; int main() { scanf("%d%d%d",&n,&m,&k); for(int i=2;i<=n;i++)//注意i从2开始 scanf("%d",&d[i]); for(int i=1;i<=m;i++) {scanf("%d%d%d",&ck[i].time,&ck[i].st,&ck[i].aim); wait[ck[i].st]=max(wait[ck[i].st],ck[i].time);//处理每个点的等待时间 goal[ck[i].aim]++;//统计每个点到达的人数 } for(int i=2;i<=n;i++) {arr[i]=max(arr[i-1],wait[i-1])+d[i]; } while(k)//开始使用加速器 { max_yx=0;max_i=0; memset(yx,0,sizeof(yx));//一定一定要写 for(int i=n;i>=2;i--)//倒着写递推求yx,可以减少一重循环 { if(d[i]==0){yx[i]=0;}//如果有d被减到了0,就肯定不能再减了,所以也就不会造福人了 else {if(arr[i]>wait[i]) {yx[i]+=goal[i]; yx[i]+=yx[i+1];//这样的i可以影响到i+1 if(yx[i+1]==0&&wait[i+1]==0) yx[i]+=yx[i+2];//注意这里,如果某个点i+1既没有人要去,又没有人的起点是它,那么arr[i+1]一定大于wait[i+1],而且yx[i]是可以加上yx[i+2]的,所以要做特判(这个点值20分,题解里有的没有写qwq)说实话应该再来个循环判断的,但是我懒qwq } else yx[i]=goal[i];//如果无法影响到i+1,那么造福的人数就只有到达i的人 } } for(int i=1;i<=n;i++)//选最大 {if(yx[i]>max_yx) {max_yx=yx[i]; max_i=i; } } if(max_i==0)break; d[max_i]--; k--; for(int i=max_i-1;i<=n;i++)//简单粗暴的维护 arr[i]=max(arr[i-1],wait[i-1])+d[i]; } int sum=0; for(int i=1;i<=m;i++) { sum+=arr[ck[i].aim]-ck[i].time; } printf("%d ",sum); }


这两个人轮流来,所以在决策的时候就很麻烦,而且没有后效性。所以我们把A和B的决策算做一步。这样决策就有后效性了。

设每经过一遍决策之后到达的城市与当前所在的城市连一条边,那每个城市只有一条出边,这就是棵平衡树。dalao都说用双向链表什么的,可惜我只见过set。
我们从出发点往上跳,看能否跳到终点,当在每一层最大的边权大于x的时候就不能跳了。这里我们用树状倍增处理。
树状倍增:
设fa[i][j]表示i的第2^j个祖先。max[i][j]=max(i,fa[i][j])表示i到fa[i][j]的最大边权。二分比较。

二分答案+check。(仿佛看见当年跳石头的影子)为什么捏?你看这毒瘤数据范围,又大又圆。
怎么检查?
检查点建立的越接近首都,覆盖的路径就越多。所以我们希望检查点都建立在首都的儿子节点上。
但是有的军队可能不能在t的时间内走道首都的儿子节点,那我们不动它,把所有军队能走道的节点标记下来。每个标记的节点的子树就被控制住了。但如果还有节点没有封住,怎么办?(就像下面这样)
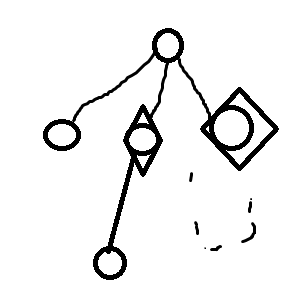
我们先假设军队在建造完成之后还可以移动。每个的剩余移动时间为d[i],让最少的不再移动,让其他的移动到首都。再通过首都移动到没有覆盖住的点。这样我们按照剩余时间排序,看军队是否能覆盖剩余检查点。

思路:最短路。(因为最少时间啊)老师表示这玩意就是n个拼起来不想讲
暴力预处理每个状态,然后跑最短路(如果图不连通,就无解)


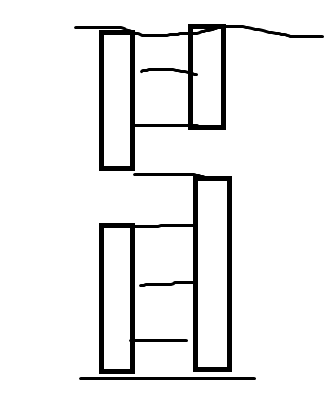
我们像上面这样把屏幕分成几个格子,看小鸟能到达哪些格子。


依旧是二分时间+判定。
二分答案后就是考虑树上两个点的距离是否小于某个数。(不加虫洞)(用树状倍增)
来我们加上虫洞。
在不加虫洞时,有些能完成,而有些完不成。要保证都能完成,我们把虫洞放在完不成的路径的交上。(选权值最大那条边)放完之后看能否都能完成。
details:
找交:看路径是否被覆盖n次。我们覆盖路径的时候,因为每次路径的次数要+1,暴力加复杂度就炸了。所以我们用前缀和的方式来整。

空间???真是鬼畜。(玄学)
开a[100]记录???
正解:设
number ,prenumber, count
if(number!=prenumber)count--;
else count++;
if(count==0)prenumber=number;
ans=prenumber;
prenumber是上一个读入的数,number是当前读入的数,重复这个玄学操作一直到最后。
这里的数据保证有解。(因为这个正解算法判不了无解,如果有毒瘤数据就裱出题人好了(小姐姐说的qwq))

首先,你建不出来补图
妈耶我又凉了
如果两个点之间没有边,那么它在补图里有边。如果有边,那在补图里就没有边。
从1开始,把和它没有边关系的点加入队列。一个一个处理队列里面的点。当队空时,就处理完了一个联通块。如果还有没有入队过的点,就从这个点开始,进行相同的操作。直到所有点都入过队。
我们考虑一下优化。用链表。
