最小生成树

什么是最小生成树呢？

在此先说一下什么是树。

树是图的一种，是无向无环联通图。意思是：首先，树是无向图，其次，不会形成环，且是连通图（从一个点可以到达其他所有的点）

举个栗子

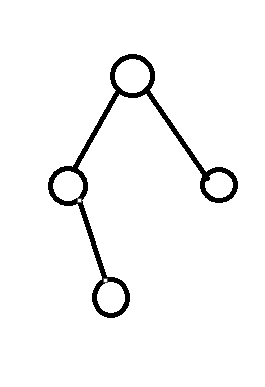
这就是一颗树

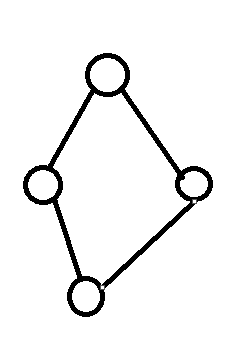
这样就不是了，因为形成了环 。

树分为有根树和无根树

有根树：明确两个点的父子关系（可以认为所有边是有向的，由父亲指向儿子或相反）

无根树：没有明确的父子关系，指定任意一个点当做跟都可以，但在指定跟以后，就变成了有根树。

生成树：若图中有n个点（这张图里有6个），从图中选出n-1条边（这里就是选5条）构成一个树，即称为该图的生成树。

最小生成树：生成树中边权之和最小的生成树。

算法一：

prim

  prim和dijkstra算法的思想比较像，每次添加没有添加过的，到当前的生成树距离最小的边（用d[i]记录点i到生成树的距离）。在这里默认①为根节点。将当前边权之和（ans）加上该边的权值，同时标记这条边的终点i（这里的“终点”是以生成树（把它视作一大坨点）为起点，边的终点）已经加入进生成树。一直找到最后，如果刚好找到n-1条边，那最终答案就是ans。（有的数据会让你找不到合适的可以加入的边）

  prim是以点为单位加入而不是以边为单位，所以用邻接矩阵存图即可（用前向星会TLE），适用于点少边多的数据。

//代码from wz
#include <bits/stdc++.h>
using namespace std;
int n, m;
int t[5001][5001];
int d[5001];
bool vis[5001];
int ans, cnt;//ans为边权之和,cnt为当前的边数
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
            t[i][j] = 1000000005;//初始化为无限大
        t[i][i] = 0;
    }
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        t[v][u] = t[u][v] = min(t[u][v], w);//对于不能直达的两个点来说，它们当前的距离是无限大，
//并且若数据不断更新这条边，总能保证这个边的边权保持最小（数据可能会出现重边）（模板题血与泪的教训）
    } 
    for (int i = 1; i <= n; i++)
    {
        d[i] = 1000000005;//初始化 
    }
    for (int i = 1; i <= n; i++)
    {
        d[i] = t[1][i];//记录最开始到当前生成树（只有根节点 ①的树）的距离 
    }
    d[1] = 0;
    vis[1] = 1;
    while (cnt <= n - 1)
    {
        int min_i = 0, min_d = 1000000005;//min_d寻找当前可以加入的边权最小的边
        for (int i = 1; i <= n; i++)
        {
            if (!vis[i] && d[i] < min_d)//判断是否合法
            {
                min_d = d[i];
                min_i = i;//min_i记录这条边的终点
            }
        }
        if (min_i == 0)//如果找不到就跳出循环
        {
            break;
        }
        cnt++;//已经加入的边数加一
        ans += min_d;
        d[min_i] = 0;//i已经加入进生成树，所以i和生成树的距离是0
        vis[min_i] = 1;//标记i已经加入了
        for (int i = 1; i <= n; i++)
        {
            d[i] = min(d[i], t[min_i][i]);
        }
    }
    if (cnt == n - 1)
    {
        cout << ans << endl;
    }
    else
    {
        cout << -1 << endl;
    }
}

算法二：

kruskal 

 本质和prim差不多，都是加入当前的最小边。kruskal算法先将所有边从小到大排序，看加入每条边后是否成环，如果成环就不取，不成环就取。

 思想好理解，重点在于如何判环。

 这里我们要用到并查集。将所有已经加入的边的端点放入同一个集合中，再加入边时，只需要判断这条边的起点和终点是否在同一集合里（如果在，加入后就会形成环）。

//代码from最最美丽的wz小姐姐
#include<bits/stdc++.h>
using namespace std;
struct edge{
    int from,to,dis;
}g[500001];
bool cmp(edge a,edge b){
    return a.dis<b.dis;
}
int fa[200001];
int getf(int x){//并查集的并 
    if(fa[x]==x)return x;
    fa[x]=getf(fa[x]);
    return fa[x];
}
int n,m,cnt;
long long ans;
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>g[i].from>>g[i].to>>g[i].dis;
    }
    for(int i=1;i<=n;i++){
        fa[i]=i;//并查集初始化 
    }
    sort(g+1,g+m+1,cmp);//将边排序 
    for(int i=1;i<=m&&cnt<=n-1;i++){
        int fu=getf(g[i].from),fv=getf(g[i].to);
        if(fu==fv)continue;//如果要加入的边的起点和终点已经在生成树里了，就不加入 
        fa[fu]=fv;//加入后合并两点 
        cnt++;//总边数+1 
        ans+=g[i].dis;//答案加上边权 
    }
    if(cnt==n-1){
        cout<<ans<<endl;
    }else{
        cout<<"No Solution.
";
    }
}