搜索里有深搜,又有广搜,而广搜的基础就是队列。
队列是一种特殊的线性表,只能在一段插入,另一端输出。输出的那一端叫做队头,输入的那一端叫队尾。是一种先进先出(FIFO)的数据结构。
正经的队列:
头文件:#include <queue>
入队:q.push(要入队的数)
返回第一个元素:q.front( )
从队列中移除第一个元素:q.pop( )
查看队列中元素的个数:q.size( )
返回队列的最后一个元素:q.back( )
用数组模拟的队列:
可以定义数组q[100001](可大可小)
队头为head,队尾为tail
注意:
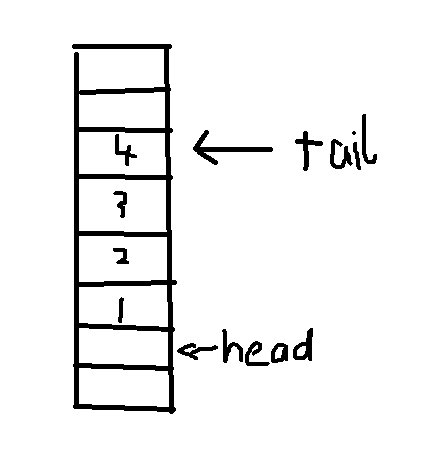
如图,head指向第一个实际元素的前一个位置,tail指向最后一个实际元素的位置
无论数组多大,总会有个界限,入队过多会溢出,而前面出队时会有空出来的位置,所以我们可以把一个数组循环使用。
代码如下:
void rudui(int x) {tail++: if(tail==n+1) tail=1; if(tail==head)//入队要判满 {printf("操作无效,队列已满"); return;} q[tail]=x; }
说了些基本定义,再来说说应用。
队列的应用和广搜是分不开的。
那什么是广搜?
就是一层一层的搜索,从第0层开始,每层都枚举出可能的情况,直到找到符合要求的情况为止
如图:

放个模板
这里是用数组模拟队列 int bfs() { 队列初始化; head=0;tail=1;//记住tail指向最后一个实际元素!! do{ head++;//head指向带扩展节点 for(int i=1;i<=max;i++)//节点如何扩展 { if(子节点符合条件) {tail++;该节点入队; if(与原来有重复) { 删除该节点;tail--; } else {if(找到目标)输出并退出; } } } }while(head<tail);//队列不空就继续搜索 }
举个栗子:
例题1:
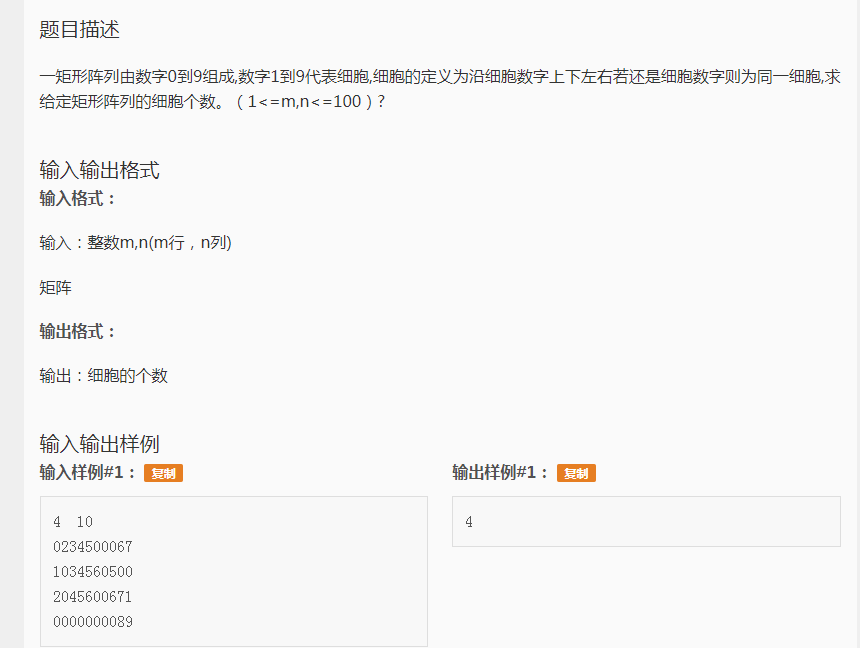
这个题就是广搜的典型例题。
在这道题中,所有非0数都可以看做是1,因为它们的值不影响判断。这样就可以用一个bool数组a[1001][1001]来表示这个矩阵
通过样例可以知道,矩阵的输入是没有空格的,所以要用字符型输入(这是个坑)
既然我们决定用bool型数组(只有0,1),而且还有前面那个坑。为了防止毒瘤的非法读入,我们先将整个a数组置为1。我们输入时判断一下,如果输入的字符是0,就把对应位置置为0。
然后就是搜索了。
先在main里找到1,再进行搜索,会省时间。
搜索时,记录下当前的i,j。从i,j的上下左右搜索,如果是1,就将这个位置的坐标放入队中,并将这个位置置为0,防止重复
入队的同时将队头出队,一直到队空为止,完成一次搜索,计数器加1.
代码如下:
#include<iostream> #include<cstdio> using namespace std; int n,m,num,dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};//预处理出4个方向 bool a[101][101]; void justdoit(int p,int q) { a[p][q]=0; int x,y,head,tail,i; int h[10001][3]; num++; h[1][1]=p;h[1][2]=q;//h[head][1]为横坐标,h[head][2]为纵坐标 head=0;tail=1; do{ head++; for(int i=0;i<=3;i++) {x=h[head][1]+dx[i];y=h[head][2]+dy[i]; if((a[x][y])&&(x>=0)&&(y>=0)&&(x<m)&&(y<n)) {tail++; h[tail][1]=x;//坐标入队 h[tail][2]=y; a[x][y]=0; } } }while(head<tail); }//其实就是套模板 int main() {char c[101]; scanf("%d %d",&m,&n); for(int i=0;i<=m-1;i++) {for(int j=0;j<=n-1;j++) a[i][j]=1; } for(int i=0;i<m;i++) { scanf("%s",c); for(int j=0;j<n;j++) {if(c[j]=='0'){a[i][j]=0; } } } for(int i=0;i<m;i++) {for(int j=0;j<n;j++) if(a[i][j])justdoit(i,j); } printf("%d",num); }
例题2:

这个题显然没有什么数学规律可以解方程什么的,所以我们好像只能搜索了。
从a,b两点搜索到1会造成一些时间的浪费,因为(1,1)在棋盘的一角,而a和b在棋盘中间,会造成在左下角方向的浪费
如图:
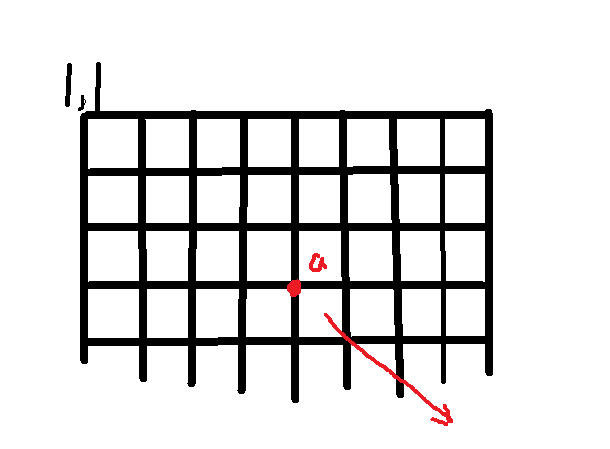
如果从a搜索到(1,1),会造成在箭头方向上的浪费,所以我们从(1,1)开始搜,搜到a停止
这里有两个点,参照对a的搜索方式,我们可以a,b一起搜。
先用p[101][101]数组将棋盘表示出来,所有的p[i][j]都初始化为-1,表示都没有到过
同时用dl[100001][4]数组来模仿队列,记录当前的所有到过点的坐标
其中dl[i][1]为横坐标,dl[i][2]为纵坐标,dl[i][3]为到达当前坐标所用最小步数
边界:点的横纵坐标大于0
一旦到达a和b,输出并结束程序
代码如下:
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; int ax,ay,bx,by,dx[12]={-2,-2,-1,-1,2,2,1,1,-2,-2,2,2},dy[12]={-1,1,-2,2,-1,1,-2,2,-2,2,-2,2}; int numa,numb; int main() { scanf("%d%d%d%d",&ax,&ay,&bx,&by); int dl[100001][4]={0}; int p[101][101]; dl[1][1]=1;dl[1][2]=1;dl[1][3]=0;//这里从(1,1)开始跳,跳到a,b两点坐标结束(???) memset(p,0xff,sizeof(p));//dl[i][3]记录跳到(dl[i][1],dl[i][2]的步数) p[1][1]=0;//用p数组表示棋盘上的每个点,到过就+1,初始为-1(方便统计只到过一次的点) int head=1,tail=1; while(head<=tail) { for(int i=0;i<=11;i++) {int x=dl[head][1]+dx[i],y=dl[head][2]+dy[i];//12个方向 if(x>0&&y>0)//若从(1,1)开始跳,则不能超出棋盘 { if(p[x][y]==-1)//之前没有到过这个点 {p[x][y]=dl[head][3]+1;//到达点(x,y)所需要的步数p为跳到上一个(x,y)的步数再加一 tail++; getchar(); dl[tail][1]=x;//记录坐标 dl[tail][2]=y; dl[tail][3]=p[x][y];//记录跳到(x,y)的步数 } if(p[ax][ay]>0&&p[bx][by]>0)//肯定不可能0步就跳到 {printf("%d %d ",p[ax][ay],p[bx][by]); return 0; } } } head++; } }