1229: Rational Resistance
Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 8 Solved: 4
[Submit][Status][Web Board]
Description
Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.
However, all Mike has is lots of identical resistors with unit resistance R0 = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:
- one resistor;
- an element and one resistor plugged in sequence;
- an element and one resistor plugged in parallel.
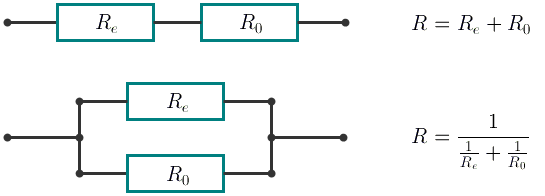
With the consecutive connection the resistance of the new element equals R = Re + R0. With the parallel connection the resistance of the new element equals 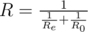 .
In this case Reequals the resistance of the element being connected.
.
In this case Reequals the resistance of the element being connected.
Mike needs to assemble an element with a resistance equal to the fraction  .
Determine the smallest possible number of resistors he needs to make such an element.
.
Determine the smallest possible number of resistors he needs to make such an element.
Input
The single input line contains two space-separated integers a and b
(1 <= a, b <= 1^18). It is guaranteed that the fraction  is
irreducible. It is guaranteed that a solution always exists.
is
irreducible. It is guaranteed that a solution always exists.
Output
Print a single number — the answer to the problem.
Please do not use the %I64d specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the%lld specifier.
Sample Input
Sample Output
HINT
In the first sample, one resistor is enough.
In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance 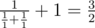 .
We cannot make this element using two resistors.
.
We cannot make this element using two resistors.
Source
题意:就是去找最少要多少个电阻能够达成功能。
思路:假设 a/b > 1 则 a/b 整数部分能够加到ans。a再模b。 假设a == b 则ans += a , a变为0; 假设 a/b < 1 则b/a 整数部分能够加到ans。b再模a
比如:3/5 要先变为1 / ( 2 / 3 +1 ) ,ans=1。然后变为 1 / ( 1 / 2 + 1 ) 。 ans=2,最后1 /(1 + 1),ans =4
AC代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
int main()
{
ll a, b;
while(scanf("%lld %lld", &a, &b)!=EOF)
{
ll ans = 0;
while(a)
{
if(a > b)
{
ll t = a / b;
ans+=t;
a=a%b;
}
else if(a == b)
{
ans+=a;
a=0;
}
else if(a < b)
{
ll t = b / a;
ans+=t;
t = b;
b = a;
a=t%a;
}
}
printf("%lld
", ans);
}
return 0;
}
版权声明:本文博客原创文章,博客,未经同意,不得转载。